Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 25.Exercício - Ex. 35

Faça uma mudança de coordenadas conveniente para concluir que Ω : z = x y é um paraboloide hiperbólico e esboce-o.

Passo 1

Temos uma quádrica com termo misto! E agora? O que fazemos???

Calma, não se assustem, é simples. Vamos repetir todo o procedimento que fizemos com cônicas para eliminação do termo misto.

Mas aí vocês devem se questionar: e a variável z ? Simplesmente, vamos que esquecer que ela é uma variável. Por que não pensamos que ela é uma constante?

Portanto, temos a seguinte “cônica”:

x y - z = 0

E para eliminar o termo misto, temos que fazer uma rotação.

Passo 2

Vamos fazer a rotação da cônica. Os seus únicos coeficientes são B = 1 e F = - z .

Calculando c o t g 2 θ , temos:

c o t g 2 θ = A - C B = 0

Portanto, θ = 45 ° . Vamos descobrir agora quem são A ' e C ' referente ao novo sistema. Logo,

A ' + C ' = A + C A ' - C ' = B sen ⁡ 2 θ ⟹ A ' + C ' = 0 A ' - C ' = 1

Resolvendo o sistema acima, obtemos A ' = 1 / 2 e C ' = 1 / 2 . Portanto, temos a seguinte “cônica” rotacionada:

1 2 x 2 - 1 2 y 2 - z = 0

Mas calma, não fica legal usarmos as mesmas letras após fazermos uma mudança no sistema de coordenadas. Então, vamos chamar

1 2 u 2 - 1 2 v 2 = w

O que corresponde a um paraboloide hiperbólico cujo eixo de simetria é O z = O w .

Passo 3

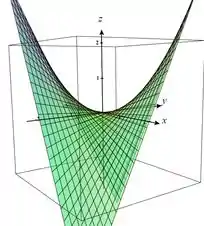
O esboço das quádricas é algo um pouco mais difícil. Aqui, iremos mostrar como ela está se comportando no geral.

O importante, é sempre colocarem o vértice dela e indicar os eixos, como ela se comporta (eixo de simetria e etc). Portanto, temos o seguinte paraboloide:

Resposta

Ao fazermos a mudança de coordenadas, obtemos:

1 2 u 2 - 1 2 v 2 = w

O que corresponde a um paraboloide hiperbólico cujo eixo de simetria é O z = O w . Além disto, o esboço da quádrica é:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Prove que as equações x 2 a 2 - y 2 b 2 - z 2 c 2 = 1 e - x 2 a 2 - y 2 b 2 + z 2 c 2 = 1 descrevem hiperboloides de duas folhas, esboce-os e estabeleça uma relação entre os sinais do primeiro membro
Justifique a afirmação feita na Observação 25-2(a). Examine as simetrias da quádrica Ω : x 2 + y 2 + 3 z 2 - 2 x y - 7 = 0 , em relação à origem, aos eixos coordenados e aos planos coordenados. Repita
Seja Ω : x 2 a 2 + y 2 b 2 - z 2 c 2 = 1 um hiperboloide de uma folha. Prove que, se a ≠ b , toda as elipses contidas como interseção de Ω com planos paralelos a O x z são semelhantes. Prove que, se k
Seja Ω a quádrica de equação 4 x 2 + y 2 + 4 z 2 - 8 x - 4 y - 8 z + 8 = 0 . Complete quadrados para provar que Ω é um elipsoide. Faça uma translação do sistema de coordenadas para eliminar os termos
Nos casos em que a intersecção do plano π com o elipsoide Ω for uma elipse, determine seu centro, focos, vértices e excentricidade. Se for uma circunferência, determine o centro e o raio. Ω : x 2 64 +