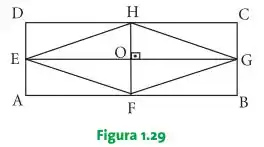
1. A figura 1.29 apresenta o losango inscrito no retângulo , sendo o ponto de intersecção das diagonais desse losango. Decidir se é verdadeira ou falsa cada uma das seguintes afirmações:

h)

Então galera, o enunciado nos pergunta se o módulo do vetor é idêntico à metade do módulo do vetor , certo? Tudo bem. Se traçarmos os vetores em questão na figura que nos foi dada, teremos:

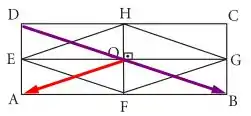
No qual o vetor em vermelho é e o vetor em roxo é . Esse módulo indica que não nos preocuparemos com a direção e sentido do vetor, e sim se eles possuem mesma intensidade, ou melhor, mesmo valor numérico!

Se observarmos com cuidado nossos vetores, notaremos que ambos estão apontando em sentidos diferentes, não é mesmo? Um está apontando para a direita e um pouco para baixo e o outro está apontando para a esquerda e um pouco para baixo também. Além disso, a direção dos vetores também são diferentes. Como o retângulo é uma figura simétrica, galera, então temos que o segmento de reta corta nosso retângulo exatamente ao meio! Sendo assim, temos que o vetor forma uma diagonal completa do retângulo, enquanto forma meia diagonal do retângulo. Sendo assim, podemos afirmar que:

Portanto, temos que a afirmação é verdadeira!