Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 18.Exercício - Ex. 15
Um hexágono regular contido em tem centro e seu lado mede . Determine seus vértices sabendo que dois deles pertencem a .
Passo 1
Queremos achar os vértices de um hexágono regular cujo lado é , contido no plano e com centro . Assim, seja um vértice genérico desse tetraedro. Devemos ter
Assim,
Além disso, como se trata de um hexágono regular, a distância de cada vértice ao centro é igual ao lado do tetraedro:
Assim, como :
Portanto,
Juntando os termos
Essa equação da o conjunto dos pontos que estão no plano e distam de . Os vértices do hexágono estão nesse conjunto!
Passo 2
Sabemos também que dois dos vértices do hexágono estão na reta . Assim,
Obviamente, essa reta deve estar contida no plano , já que dois de seus pontos estão nele! Tiramos de cara que . Substituindo na equação do passo 1:
Assim, achamos
Obtemos então dois vértices:
Vamos calcular a distância entre esse dois pontos:
Note que a distância é o dobro do lado do hexágono. Além disso, note que é o ponto médio entre e . Assim, e representam vértices opostos do hexágono!
Passo 3
Vamos fazer um esboço do hexágono para nos localizarmos melhor:
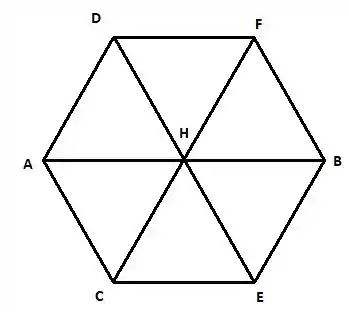
Vamos atrás agora dos pontos e cuja distância até seja . Esses pontos devem ser da forma com :
Portanto,
Logo,
Ou ainda,
Desta forma, queremos resolver o sistema
Subtraindo a primeira equação pela segunda:
Portanto, os pontos e são do tipo
Passo 4
Vamos olhar agora para a distância entre e :
Usando a lei dos cossenos:
Assim,
Assim, as distância de e até são . Portanto, usando que esses pontos são da forma e :
Logo,
Assim,
Resolvendo essa equação do segundo grau:
Assim,
Passo 5
Faltam os pontos e . Para achar eles, vamos usar que é ponto médio entre e e entre e :
Assim,
Portanto,
Logo,