Identificar as seguintes cônicas:
Passo 1
A questão pede para identificarmos a cônica cuja equação foi dada.
Neste caso, temos
Dividindo a equação por :
Trata-se de uma elipse centrada na origem com eixo maior na direção !
Passo 2
Um esboço da cônica é dado a seguir:
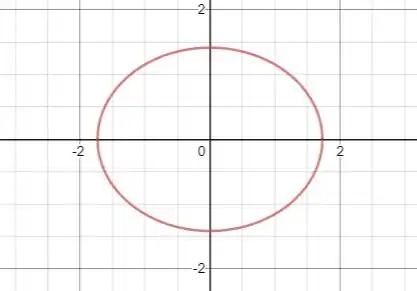
Resposta
Elipse