Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 16.Exercício - Ex. 26d

Sejam π 1 : a 1 x + b 1 y + c 1 z + d 1 = 0 e π 2 : a 2 x + b 2 y + c 2 z + d 2 = 0 planos transversais, e r sua interseção.

(d) Utiliza a equação do feixe incompleto para obter o plano π que contém a reta interseção dos planos π 3 : x + y - 1 = 0 e π 4 : x + 2 y - 1 = 0 e que determina com os eixos coordenados um tetraedro de volume 1 / 12 (o sistema é ortogonal).

Passo 1

Para começarmos a resolução, vamos considerar os planos transversais π 3 e π 4 , cuja interseção define a reta r . Além disso, um outro plano π contém tal reta e, ainda, forma um tetraedro B A C O com os eixos coordenados. Vamos fazer uma ilustração da última situação para facilitar a visualização:

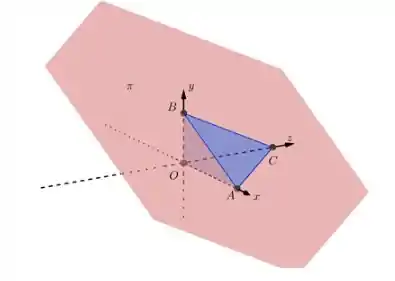
Passo 2

Dessa forma, nossos cálculos partirão da equação do feixe de planos que passam por uma reta, demonstrada nos itens anteriores. Assim, como os planos π ,   π 3 e π 4 fazem parte do mesmo feixe de planos, temos:

π : x + 2 y - z - 1 + λ x + y - 1 = 0 ⇒ x 1 + λ + y 2 + λ + z - 1 - 1 + λ = 0

Passo 3

A seguir, vamos definir os pontos do tetraedro, tais que: A = ( a ,   0,0 ) B = ( 0 ,   b ,   0 ) C = ( 0 ,   0 ,   c )

Sabendo que tais pontos pertencem ao plano π , vamos expressar suas coordenadas em função de λ , utilizando a equação geral do plano. Dessa forma, temos:

a 1 + λ = ( 1 + λ ) b 2 + λ = ( 1 + λ ) b - 1 = 1 + λ           ⇒ a = 1                               b = 1 + λ ( 2 + λ )         c = - ( 1 + λ )

Passo 4

Basta agora, desenvolver a relação do volume do tetraedro B A C O . Temos, então:

V B A C O = 1 3 . A C A O . H

1 12 = 1 3 a . c 2 . b

a . c . b = 1 2    

Passo 5

Por fim, faremos um sistema com os dados obtidos até aqui, com o objetivo de achar o valor de λ :

1 = 2 . a . c . b a = 1                                           b = 1 + λ 2 + λ                     c = - 1 + λ               ⇒ 2 . 1 . 1 + λ 2 + λ . - 1 + λ = 1   2 . 1 + λ . 1 + λ = 2 + λ                         2 + 2 λ 2 + 4 λ = 2 + λ             2 λ 2 + 3 λ = 0             ⇒ λ = 0     o u     λ = - 3 2

Ou seja, o plano π é dado por:

π :   λ = 0       λ = - 3 2 ⇒ x 1 + 0 = y 2 + 0 + z - 1 - 1 + 0 = 0 x 1 - 3 2 = y 2 - 3 2 + z - 1 - 1 - 3 2 = 0 ⇒ x + 2 y - z - 1 = 0 x - y + z - 1 = 0    

Resposta

π :   x + 2 y - z - 1 = 0 x - y + z - 1 = 0    

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre uma equação de plano para um plano que contenha os pontos 0,1 , 1 , ( 1,0 , 1 ) e ( 1,1 , 0 ) .
Encontre uma equação de plano para um plano que passe pelo ponto ( 1 , - 1 , - 1 ) e seja paralela ao plano 5 x - y - z = 6 .
Encontre uma equação de plano para um plano que contenha a origem e os pontos 3 , - 2,1 e ( 1,1 , 1 ) .
Encontre uma equação de plano para um plano que passe pelo ponto - 1 , 1 2 , 3 e seja perpendicular ao vetor ( 1,4 , 1 ) .
Encontre uma equação de plano para um plano que passe pelo ponto 1 , 1 2 , 1 3 e seja paralela ao plano x + y + z = 0 .