Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 2ª Edição - Alfredo Steinbruch e Paulo Winterle- Ed: 2º - Capítulo 4.8 - Ex. 35
Mostrar que a matriz do operador linear identidade
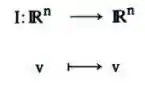
em uma base qualquer, é a matriz identidade .
Passo 1
A questão pede para mostrarmos que não importa em qual base, a matriz de transformação do operador indentidade é a matriz identidade.
Por simplicidade, vou fazer no caso , mas a generalização é imediata.
Seja uma base qualquer para . Temos que e .
Passo 2
Pela transformação linear, temos que
Assim, a matriz de transformação na base será
Vemos que se trata da matriz identidade!
Passo 3
Para generalizar para uma dimensão qualquer, basta tomar:
Para uma dado entre e , teremos que , em que todas as componentes são , exceto a i-ésima componente, que será . Construindo a matriz de transformação, teremos exatamente a identidade!
Resposta
Demonstração.
Exercícios de Livros Relacionados
Considere o operador linear F do R 3 definido por F ( 1 ,0 ,0 )=( 1 ,1 ,1 ) , F ( 0 ,1 ,0 )=( 1 ,0 ,1 ) eF 0 ,1 ,2=( 0 ,0 ,4 ) . F é invertíıvel? Se for, determine o isomorfismo inverso.
Provar que o R 2 é isomorfo a qualquer sub-espaço de dimensão 2 do R 3 .
Seja F :R 3 → R 3 definida por F ( 1 ,0 ,0 ) = ( 1 ,1 ,0 ) e F ( 0,0 ,1 )=( 0 ,0 ,2 ) e F 0 ,1,0 = ( 1 ,1 ,2 ). Determinar uma base de cada um dos seguintes sub-espaços vetoriais: K e r ( F ), I m ( F
Seja e 1 , … , e n a base canônica do R n . Seja F : R n → R n o operador linear dado por F e 1 = e 2 ,F e 2 = e 3 , … , F e n = e 1 . Determinar F x 1 , … , x n e verificar se F é um automorfismo. Se
Consideremos uma transformação linear F : U → V . Se dim Udim V , prove que existe um vetor não nulo u 0 ∈ U tal que F u 0 = 0 (vetor nulo de V ). (Ou seja, F não é injetora.)