Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 3.10 - Ex. 21

Mostre que a área do triângulo na figura é dada pelo determinante:

1 2 x 1 y 1 1 x 2 y 2 1 x 3 y 3 1

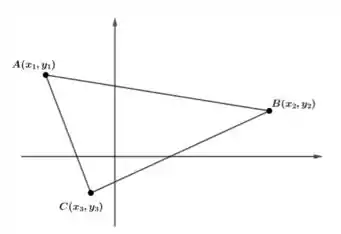
Passo 1

Basicamente, vamos encontrar a reta suporte de A B e a distância de C à essa reta, que é a altura relativa ao lado A B . Depois é só calcular o lado A B e finalizar o exercício.

Passo 2

Da geometria analítica, temos que a equação da reta que passa por A B é dada por:

x 1 y 1 1 x 2 y 2 1 x y 1 = 0 ⇒ y 1 - y 2 x - y x 1 - x 2 + x 1 y 2 - x 2 y 1 = 0  

Fazendo a distância de C à essa reta:

h A B = y 1 - y 2 x 3 - y 3 x 1 - x 2 + x 1 y 2 - x 2 y 1 y 1 - y 2 2 + x 1 - x 2 2  

Mas:

y 1 - y 2 2 + x 1 - x 2 2 = A B

Ou seja:

h A B = y 1 - y 2 x 3 - y 3 x 1 - x 2 + x 1 y 2 - x 2 y 1 A B   ⇒

⇒ h A B A B = y 1 - y 2 x 3 - y 3 x 1 - x 2 + x 1 y 2 - x 2 y 1

Aproveitando o determinante mais acima, podemos escrever o lado direito na nossa equação como sendo:

x 1 y 1 1 x 2 y 2 1 x 3 y 3 1

Logo:

h A B A B = x 1 y 1 1 x 2 y 2 1 x 3 y 3 1

Passo 3

Lembrando que a área é b a s e × a l t u r a 2 , temos:

Á r e a   d o   t r i â n g u l o = h A B A B 2 = 1 2 x 1 y 1 1 x 2 y 2 1 x 3 y 3 1

Resposta

Demonstração.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja A = a b c d e f g h i supondeo que det ⁡ A = - 7 , obtenha det ⁡ ( 2 A ) - 1
Em cada parte, encontre o determinante, sabendo que A é uma matriz 3 × 3 com det ⁡ A = 7 a )det ⁡ 3 A
Seja A x = b o sistema 4 x + y + x + w = 6 3 x + 7 y - z + w = 1 7 x + 3 y - 5 z + 8 w = - 3 x + y + z + 2 w = 3 . Resolva o sistema por eliminação de Gauss-Jordan
Provar que det ⁡ 1 a 2 a 3 1 b 2 b 3 1 c 2 c 3 = det ⁡ b c a a 2 c a b b 2 a b c c 2
Seja A = a a ⋮ a ( bb … b ) Quanto é d e t ⁡ ( A ) ?