Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 24.Exercício - Ex. 27
Obtenha uma equação da superfície cônica de vértice , circunscrita a superfície esférica
Passo 1
Escrevendo a equação reduzida dessa esfera nós temos:
Completando os quadrados dessa expressão nós teremos:
Passo 2
Aí a parada para essa questão é considerar que esse ponto é exterior a e que existe um ponto que pertence a superfície que é cônica somente se pertence a uma reta tangente a essa esfera, então considerando um ponto de tangência nós temos que:
Onde é uma vez que é a origem:
Aplicando na esfera nós teremos:
O que nos dá uma equação de:
Passo 3
Fazendo o determinante dessa equação ser zero (para termos a tangente) nós obteremos:
Ou algo como:
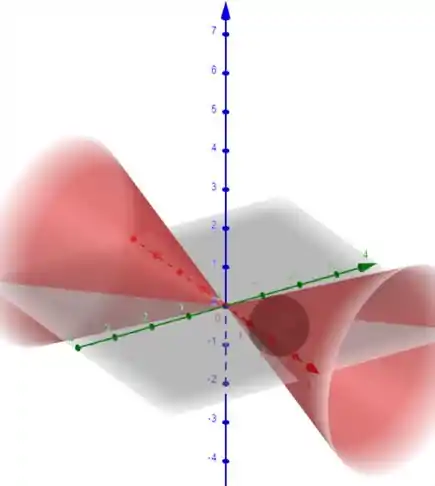
Plotando a região e a esfera nós teremos algo como:
Resposta
Exercícios de Livros Relacionados
Determine a superfície esférica de menor área, tangente aos três planos coordenados e passando pelo ponto P =( 1 ,- 5 ,- 4 ) .
Determine o centro e o raio da circunferência, interseção do plano 2 x- y+ 3 z-3=0 com a superfície x 2+y 2+ z 2- 2 y- 2 z- 2=0 .
Determine as coordenadas das extremidades do diâmetro da superfície esférica e que é paralelo a reta x+ 1 =- y +5=z -7 .
Ache os planos que passam pela reta t : ( x , y , z )=( 4,5 , - 2 )+m ( 1 , - 1,0 ) e que cortam sobre a superfície esférica S :( x - 1 ) 2+( y - 2 ) 2+ ( z - 1 ) 2 = 16 circunferências de raio 7 .
Dada a superfície esférica x 2 + y 2 + z 2 - 3 x - 9= 0 e o plano x+ y + z - 1 = 0 ,determine a posição relativa da superfície e o plano;se o plano for:externo, calcule a distância do centro ao plano;