Obtenha uma equação vetorial da reta paralela ao plano π : 2 x - y - z + 1 = 0 , concorrente com as retas r : X = 1 ,0 ,0 + λ ( 1 ,1 ,0 ) e s : X = 0 ,1 ,0 + λ ( 0 ,1 ,1 ) , que forma com elas ângulos congruentes.

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 19.Exercício - Ex. 7

Obtenha uma equação vetorial da reta paralela ao plano , concorrente com as retas e , que forma com elas ângulos congruentes.

Passo 1

Vamos chamar de a reta que queremos encontrar, (vetor diretor de ), (vetor diretor de ).

tem um vetor diretor , agora vamos analisar as informações que temos:

- Se é paralela ao plano , ela é ortogonal ao seu vetor normal, ou seja:

Passo 2

- Vamos chamar de o ângulo entre e , calculando o ângulo entre seus vetores diretores:

- Mas o enunciado falou que a reta forma ângulos congruentes, ou seja, iguais com e , então :

Como os denominadores são iguais:

Passo 3

Substituindo em , temos

Ou seja, o vetor diretor de é do tipo

E olha só que incrível, pra qualquer valor de que colocarmos nesse vetor, vamos chegar no vetor diretor correto cara!! Porque vai ser sempre LD e tal hahaha

Então vamos escolher nosso vetor diretor como , pode ser?

Passo 4

Agora vamos estudar o fato de nossa reta ser concorrente com e com .

Seja um ponto de , ponto da reta (pela sua equação), ponto da reta (pela sua equação também haha), temos:

Para que e sejam concorrentes, a trinca deve ter determinante igual a 0:

Passo 5

Somando as equações e , temos

Substituindo na equação :

Então, podemos “escolher” o ponto de que vamos usar na nossa equação desde que e .

Seja , temos e , e o ponto será

Logo, uma das equações da nossa reta é

Lembrando: há varias maneiras de escrever essa equação, a sua pode estar certa. É só conferir se os vetores são LI e se seu ponto pertence à reta acima.

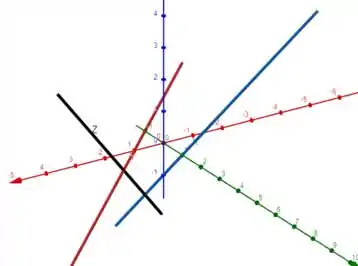
Abaixo temos em vermelho a reta , em azul a reta e em preto a nossa querida reta :)

Resposta

Lembrando: há varias maneiras de escrever essa equação, a sua pode estar certa. É só conferir se os vetores são LI e se seu ponto pertence à reta acima. Aliás, essa reta é a mesma do gabarito do seu livro :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Obtenha uma equação vetorial da reta que forma ângulos congruentes com os eixos coordenados e é concorrente com r : 2 x - 2 = 3 y - 3 = - 2 z e s : - 1,1 , 0 + λ 5,3 , 1 .

O triângulo ABC é retângulo em B e está contido no plano π 1 : x + y + z = 1 . O cateto BC está contido no plano π 2 : x - 2 y - 2 z = 0 e o ângulo C ^ mede 30°. Dado A = 0,1 , 0 , determine B e C e c

15. Determinar o valor de n para que seja de 30 ° o ângulo entre as retas r : x - 2 4 = y + 4 5 = z 3 e s : y = n x + 5 z = 2 x - 2

14. Determinar o ângulo entre as seguintes restas:(a) r : x = - 2 - 2 t y = 2 t z = 3 - 4 t e s : x 4 = y + 6 2 = z - 1 2 (b) r :y = - 2 x - 1 z = x + 2 e s : y 3 = z + 1 - 3 ; x = 2 (c) r : x = 1 + 2

17. A reta r : x = 1 + 2 t y = t z = 3 - t Forma um ângulo de 60° com a reta determinada pelos pontos A 3,1 , - 2 e B 4,0 , m . Calcular o valor de m.