Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 18.Exercício - Ex. 26a

(a) Bom pessoal, para tentar entender esse problema, vamos dar uma olhada nas equações da reta e do plano.

O enunciado deu a equação vetorial da reta :

Por essa equação, a gente pode determinar que o vetor diretor da reta é:

E temos também a equação geral do plano:

Lembre que quando a equação geral do plano tem essa forma:

O vetor formado por é o vetor normal ao plano. Então, olhando para a equação de cima, o vetor normal a é:

Tá, usando essas informações, o que a gente consegue descobrir sobre a relação entre essa reta e esse plano?

Vamos fazer o produto escalar dos dois vetores:

O produto escalar é nulo. Então os vetores são perpendiculares:

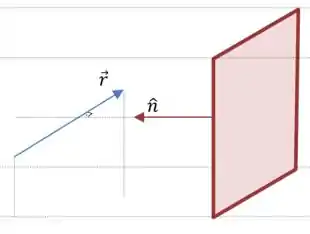
E se o vetor diretor da reta é perpendicular ao vetor normal do plano, então a reta é paralela ao plano.

Agora fica fácil resolver o problema geometricamente.

Se a gente pegar os pontos médios de todos os segmentos que ligam a reta ao plano:

Eles vão formar um plano entre a reta e o plano. Como esse novo plano tem que ser paralelo a , a equação dele é:

Essa equação, conforme o varia, é a equação do feixe de planos paralelos a .

Ou seja, os coeficiente são os mesmos, mas a constante tem que ser ajustada.

A ideia é que o novo plano esteja entre o plano e a reta .

Pela equação vetorial da reta:

Ela começa no ponto que tem coordenadas .

Qual é o plano paralelo a que contém esse ponto? É só substituir na equação geral:

Beleza, então se o plano é:

E o plano paralelo que passa pela reta é:

Então o novo plano que estamos procurando deve estar entre esse dois:

Então o novo plano é:

Ok, esse é o lugar geométrico dos pontos médios dos segmentos que vão de até .

O lugar geométrico é um plano paralelo ao plano e à reta . O plano tem equação geral e está situado entre e .