Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 17.Exercício - Ex. 7d

Obtenha equações da reta perpendicular comum às retas r e s .

r : X = 4 ,   - 1 ,   0 + λ   2 ,   - 4 ,   - 1                                             s : x + 2 z = 4 = 4 z - y - 1

Passo 1

O problema quer que achemos a reta que seja perpendicular tanto a r como a s . Primeiro vamos escrever a reta s na forma vetorial:

x + 2 z = 4 4 z - y - 1 = 4

Assim,

x = 4 - 2 z           e             y = 4 z - 5

Portanto,

x , y ,   z = 4 - 2 z ,   4 z - 1 ,   z = 4 ,   - 5 ,   0 + z   ( - 2 ,   4 ,   1 )

O vetor diretor de s é u → = ( 2 ,   - 4 ,   - 1 ) , o mesmo da reta r . Elas são paralelas! Sendo assim, existem infinitas retas que são perpendiculares às duas!

Passo 2

Mas calma meu caro jovem gafanhoto! Não é porque são infinitas retas que ainda não podemos saber qual é as suas equações! E é isso que vamos fazer aqui agora! Encontrar essas equações!

Para facilitar o entendimento, vamos fazer o seguinte: r e s são paralelas de modo que podemos essas duas retas em um mesmo plano. Agora vamos olhar para esse plano de cima pra baixo e tirar uma foto:

Agora, vamos pegar dois pontos: um em cima da reta s e outro na r :

O ponto A que está em cima da reta r pode ser dado por:

A = 4 ,   - 1 ,   0 + λ   2 ,   - 4 ,   - 1

Já o pondo B ...

B = 4 ,   - 5 ,   0 + t   ( - 2 ,   4 ,   1 )

O vetor A B então pode ser determinado facilmente fazendo...

A B = B - A = 4 ,   - 5 ,   0 + t   - 2 ,   4 ,   1 - 4 ,   - 1 ,   0 - λ   2 ,   - 4 ,   - 1

Podemos simplificar essas continhas fazendo a subtração esses vetorizinhos...

A B = B - A = 0 ,   - 4 ,   0 + t + λ - 2 ,   4 ,   1 =

- 2 t - 2 λ ,   4 t + 4 λ - 4 ,   t + λ

Agora, olhando para o desenho abaixo, repare que podemos tomar o vetor diretor da reta perpendicular como sendo A B , desde que o vetor A B seja perpendicular ao vetor diretor da reta r :

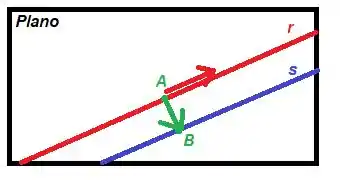
Os dois vetores, então serão perpendiculares somente se o produto escalar entre elas for igual a 0 :

2 ,   - 4 ,   - 1 ⋅ - 2 t - 2 λ ,   4 t + 4 λ - 4 ,   t + λ = 0

2 - 2 t - 2 λ - 4 4 t + 4 λ - 4 - t - λ = 0

Simplificando...

- 4 t - 4 λ - 16 t - 16 λ + 16 - t - λ = 0   →

- 21 t - 21 λ + 16 = 0     →

- 21 λ + t + 16 = 0     →

Então concluímos que...

λ + t = 16 21

O vetor A B , portanto, será...

A B = 0 ,   - 4 ,   0 + 16 21 - 2 ,   4 ,   1     →

A B = - 32 21 , 64 21 - 4 , 16 21   →

A B = - 32 21 , 64 - 4 ⋅ 21 21 , 16 21   →

A B = - 32 21 , - 20 21 , 16 21  

Com o vetor diretor em mãos, podemos dar a equação da reta perpendicular que vou chamar de p :

p : X = A + u - 32 21 , - 20 21 , 16 21

Onde u é o parâmetrod da reta e A é um ponto que pertence a essa reta. SIM! Eu não chamei de A atoa, a reta perpendicular, vai passar pelo ponto A da reta r , logo a reta p será...

p : X = 4 ,   - 1 ,   0 + λ   2 ,   - 4 ,   - 1 + u - 32 21 , - 20 21 , 16 21

Como o ponto A é um ponto qualquer da reta r , para qualquer valor de λ teremos um novo ponto A e portanto uma nova reta perpendicular (o que prova que existem de fato infinitas retas perpendiculares)

Resposta

Existem infinitas retas perpendiculares p que pode dependem do parâmetro u e de uma valor constante escolhido λ .

p : X = 4 ,   - 1 ,   0 + λ   2 ,   - 4 ,   - 1 + u - 32 21 , - 20 21 , 16 21

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache as equações da reta r que passa pelo ponto B=( 3,1 , 2 ) e é concorrente com as retas s :x + 1 1=y + 2 2 = z - 5 - 2 e t :x - 4 1=y - 1 - 1 = z - 4 - 1 .
Dadas as retas r :x - 1=y - 3 - 1 = z + 1 e ⎧x= - λ⎧ s⎢y= 1+ λ ⎢ ⎩z= 1 +2 λ⎩ ,escreva equações paramétricas da reta t , concorrente com r e s e paralela ao vetor ( - 2,1 , 1 ) .
É dado o Δ A B C com A=( 2,3 , - 1 ) , B=( 4 , - 1,5 ) e C=( 0,3 , - 1 ) .Escreva equações das três medianas.Ache a interseção de duas delas.Mostre que a terceira mediana passa pela interseção das out
As retas ⎧x=1+ 3 α⎧ b⎢ y= 1- α ⎢ ⎩ z= - 3+ 5 α⎩ ⎧ x= 1⎧ c⎢ y= 1-2 β ⎢ ⎩z=- 3+3 β⎩ passam pelo vértice A do triângulo A B C e, respectivamente, pelos vértices B e C . Determine as coordenadas de A , B
Determine a , b , c e d para que as retas r e s coincidam, sendo: ⎧ x=1+ 4 λ⎧ r⎢ y= a- 2 λ ⎢ ⎩ z= - 1+ b λ⎩ ⎧ x= 9+2 β⎧ s⎢ y= - 1+c β ⎢ ⎩z=d+3 β⎩