Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 14.Exercício - Ex. 40b
Obtenha os pontos de que pertencem ao plano , nos casos:
b)
Passo 1
Primeiro, temos que encontrar um ponto genérico da reta a partir da equação dela, esse ponto é:
Agora, é só substituirmos o ponto na equação do plano e encontrarmos qual é o que satisfaz:
Opa, nosso sumiu da conta, e obtivemos uma desigualdade pois , isso quer dizer que não existe tal que o ponto de pertença ao plano :/
Por que esse ponto não existe??
Repara o seguinte: o vetor normal do plano é ortogonal ao vetor diretor da reta , pois:
Então, a reta é paralela ao plano e portanto, eles não se cruzam nunca ;)
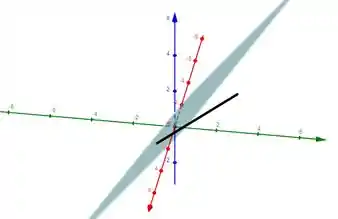
Resposta
b) Não existe intersecção entre a reta e o plano.
Exercícios de Livros Relacionados
Escreva uma equação vetorial da reta r concorrente com s , paralela ao plano π , e perpendicular à reta A B . São dados: π : 2 x - y + 3 z - 1 = 0 , A = ( 1 ,0 ,1 ) , B = ( 0 ,1 ,2 ) , s : X = 4 ,5 ,0
Determine os vértices B , C e D de um quadrado A B C D , sabendo que A = ( 0 ,- 19 ,4 ) , um lado está contido no plano π 1 : 2 x - 2 y + z = 15 , outro, no plano π 2 : 2 x + y - 2 z = 0 , e o plano d
Sejam π 1 : X = A + λ u → + μ v → e π 2 : X = B + λ w → + μ t → . Desenvolva um método para estudar a posição relativa desses planos sem utilizar equações gerais.
Mostre que a 1 a 2 + b 1 b 2 + c 1 c 2 = 0 é uma condição suficiente, mas não necessária, para que os planos π 1 : a 1 x + b 1 y + c 1 z + d 1 = 0 e π 2 : a 2 x + b 2 y + c 2 z + d 2 = 0 sejam transve
Estude a posição relativa dos planos π 1 e π 2 .c) π 1 : 2 x - y + 2 z - 1 = 0π 2 : 4 x - 2 y + 4 z = 0