Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 7.Exercício - Ex. 21
No paralelepípedo retângulo da Figura 7-4 (b), , e medem, respectivamente, , e .
a) Explique por que é base e verifique se é ortonormal.
b) Explique por que, em relação à base do item (a), .
c) Mostre que o comprimento da diagonal é .
d) Aplicando a fórmula [7-4] ao vetor , obtemos . Explique a aparente contradição.
Passo 1
O problema pede para considerarmos o paralelepípedo da figura a seguir:
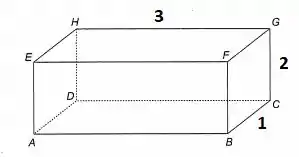
No item (a) temos que explicar por que é uma base. A resposta é simples: os três não estão num mesmo plano, sendo assim LI. Como três vetores LI sempre formam uma base, o conjunto é uma base!
Mas precisamos tomar um cuidado: essa base não é ortonormal pois a norma dos vetores não são todas igual a .
Passo 2
O vetor pode ser escrito como
Mas sabemos que e , de modo que
Passo 3
A diagonal do paralelepípedo é dada por
Assim,
Logo,
Passo 4
Usando as coordenadas do vetor e calculando sua norma, obtemos , que é diferente do comprimento da diagonal . Por que isso?
A resposta é bem simples, só podemos usar a fórmula [7-4] para a norma de um vetor se a base for ortonormal, o que não é o caso!
Resposta
Demonstrações.