Prove que existe um único ponto comum às bissetrizes internas de um triângulo e que esse ponto, conhecido como incentro do triângulo, é interior a ele.
Passo 1
Bora lá!
Primeiro, vamos fazer um esboço do nosso triângulo, onde o ponto é o incentro dele
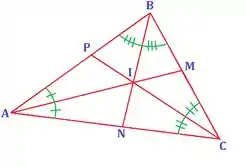
Galera, já adianto que essa é uma questão nível hard, mas vamos matar ela como os nossos “pulos do gato”. 😉
Passo 2
Para que e sejam vetores diretores das bissetrizes internas de um triângulo, devem atender as seguintes condições:
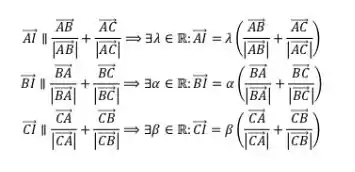
Agora vem o primeiro “pulo do gato”.
Existe um ponto comum às bissetrizes internas do triângulo ABC, SE, E SOMENTE SE,
Ou seja, os vetores não podem ser múltiplos (paralelos).
Passo 3
Inicialmente, vamos provar a primeira asserção.
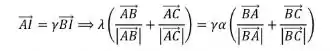
Como e são contantes arbitrárias, fazemos (nosso segundo “pulo do gato”) e vamos provar que não existe um valor de para que torne válida a igualdade.

Como , podemos reescrever da seguinte maneira

Passo 4
Beleza... acabamos de fazer um monte de conta, mas para que?
Vamos recapitular o que o nosso exercício quer?
“Prove que existe um único ponto comum às bissetrizes internas de um triângulo e que esse ponto, conhecido como incentro do triângulo, é interior a ele.”
Notem, que forem encontrados valores distintos para , certo? Então por redução ao absurdo, conclui-se que NÃO EXISTE que torne a asserção verdadeira. Portanto, e são concorrentes e interceptam-se no ponto , o incentro.
De maneira análoga, e também são concorrentes.
Pelas condições que adotamos inicialmente para que as retas sejam dissetrizes, nota-se que os vetores são múltiplos das somas de vetores diretores unitários dos lados do triângulo, portanto, a resultante dessa soma, certamente, apontará para o interior do triângulo. Daí, podemos concluir que está no interior do triângulo ABC.
Resposta
Ei, a resposta está no passo a passo :)