Sejam A = 1 ,1 ,2 ,B = 0 ,1 ,2 ,C = ( 1 ,1 ,0 ) e D = 0 ,1 ,0 , em relação a um sistema ortogonal de coordenadas de origem O .(b) Uma fonte de luz situada em O projeta sobre o plano π 1 , paralelo a π , a sombra do anteparo A B C D . Mostre que a sombra é retangular.

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 15.Exercício - Ex. 8b

Sejam e em relação a um sistema ortogonal de coordenadas de origem .

(b) Uma fonte de luz situada em projeta sobre o plano , paralelo a , a sombra do anteparo . Mostre que a sombra é retangular.

Passo 1

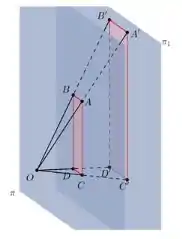
Para facilitar o entendimento da nossa questão, primeiramente, vamos construir uma figura ilustrativa da situação apresentada no enunciado:

Passo 2

Precisamos analisar a figura acima de forma bem minuciosa, assim podemos notar que, na verdade, se trata de uma pirâmide , até então com uma base desconhecida, maaaassssss que possui uma seção paralela à base, a qual determina outra pirâmide , idêntica à primeira, cuja base é o retângulo

Passo 3

Dessa forma, pela semelhança imposta no Passo 2, podemos concluir que da mesma forma que a base de é um retângulo, obrigatoriamente, a base também será um retângulo.