Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 61

Sejam e pontos distintos, pertencentes a uma elipse . Prove que as retas tangentes a em e são paralelas se, e somente se, o centro da elipse é o ponto médio de .

Passo 1

Visualmente o que temos é algo desse sentido.

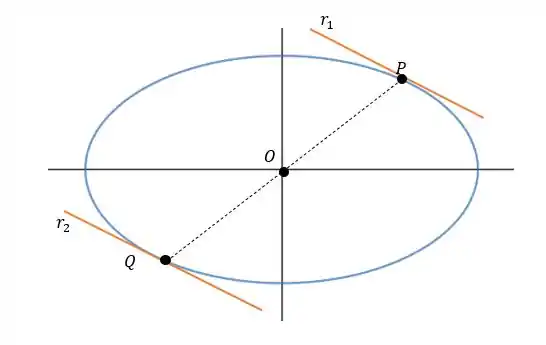
Onde as retas e são paralelas por estarem colineares os pontos , sendo o centro da elipse. Então para uma equação de elipse igual a :

Nós teremos que o determinante dessa elipse seja zero para obtermos as retas tangentes, ou seja:

Para um ponto e um vetor direcional . E note que essa condição independe se temos um vetor direção igual a ou , o sinal se corta e a igualdade é mantida. E mesmo se e esse valor tanto para quanto a direção da reta só acontece se tivermos uma reta colinear entre esses três pontos, ou seja:

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a área do losango cujos vértices são os focos e as extremidades do eixo menor da elipse de equação x 2 / a 2 + y 2 / b 2 = 1 . Em que condições esse losango é um quadrado?

Seja P um ponto da elipse E : x 2 / a 2 + y 2 / b 2 = 1 . Suponha que P ≠ B 1 e P ≠ B 2 e considere os pontos R e S de intersecção de O x com as retas B 1 P e B 2 P . Prove que O R → ⋅ O S → = a 2 . S

Determine, em função de a e b , os vértices e a área do quadrado de lados paralelos aos eixos coordenados, inscrito na elipse E : x 2 / a 2 + y 2 / b 2 = 1 . Mostre que, se os dois lados do quadrado d

Estude a natureza do ângulo sob o qual um ponto X = x ,y da elipse E : x 2 / a 2 + y 2 / b 2 = 1 vê:o eixo maior (suponha que y ≠ 0 , isto é, X ≠ A 1 e X ≠ A 2 ); o eixo menor (suponha que x ≠ 0 , ist

Seja X = x ,y um ponto da elipse E : x 2 / a 2 + y 2 / b 2= 1 , de focos F 1 e F 2 e excentricidade e . Mostre que X F 1 → ⋅ X F 2 → = e 2 x 2 + a 2 1 - 2 e 2 . Analisando o sinal de X F 1 → ⋅ X F 2 →