Sejam A = 1 ,1 ,2 ,B = 0 ,1 ,2 ,C = ( 1 ,1 ,0 ) e D = 0 ,1 ,0 , em relação a um sistema ortogonal de coordenadas de origem O .(c) Supondo que a área da sombra seja 8, determine seus vértices e obtenha uma equação geral de π 1 .

As projeções têm coordenadas A ' = 2 ,2 ,4 ,B ' = 0 ,2 ,4 ,C ' = ( 2 ,2 ,0 ) e D ' = 0 ,2 ,0 , e o plano é definido por π 1 : y - 2 = 0 .

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 15.Exercício - Ex. 8c

Sejam e em relação a um sistema ortogonal de coordenadas de origem .

(c) Supondo que a área da sombra seja 8, determine seus vértices e obtenha uma equação geral de .

Passo 1

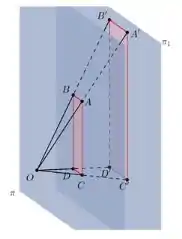
Para começarmos a nossa resolução, vamos ter que, novamente, tomar como base a figura que ilustra o enunciado:

Passo 2

Primeiramente, devemos notar que é um múltiplo de , uma vez que estão contidos em uma mesma reta, e que esta reta passa pela origem . Essa constatação pode ser generalizada para todos os vetores do sólido.

Passo 3

Assim, basta aplicarmos a relação de semelhança entre as áreas e , e os lados da figura e , para obtermos a tal constante escalar. Contudo, vamos considerar aqui e , resultados obtidos tranquilamente, já que temos todos os pontos envolvidos. Temos, então:

Ou seja, percebemos que o lado foi aumentado duas vezes. Portanto, a constante vale 2 😉.

Passo 4

Assim, devemos aplicar a constante a todos os pontos da figura, para obtermos suas respectivas projeções:

Passo 5

Por fim, sabemos que, devido aos planos e serem paralelos, suas equações seguem o MESMO FORMATO, variando apenas a constante. Ou seja, o plano é definido por . Para encontrarmos , basta substituirmos por qualquer ponto do plano, assim como fizemos no item (a), escolhendo , temos .