Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 6.Problemas propostos - Ex. 31b

Representar graficamente os planos de equações:

b) 6 x + 4 y - 3 z - 12 = 0

Passo 1

Fala galera, tudo bem? Vamos resolver junto esse exercício? =D

Pra desenhar esses planos, vamos precisar determinar onde ele corta cada eixo. Assim fica mais fácil de desenhá-lo =D

Mas, como a gente faz isso? É tranquilo, saca só!

Quando um plano corta o eixo x , por exemplo, tanto a coordenada de y quanto de z são zero. Então a equação do plano, estando na forma geral, fica:

a x + b y + c z + d = 0

E com y = z = 0 temos:

a x + d = 0

E daí a ordenada onde o plano corta o eixo x é x = - d / a . Daí esse ponto é – d a , 0,0 . Certo?

Pra achar os outros pontos é a mesma coisa: só zerar as outras ordenadas e resolver pra variável.

Achando os três pontos, colocamos ele em um sistema cartesiano e deu! Ta feito o desenho do plano!

Beleza? Vamos começar?

Passo 2

A equação do plano é:

6 x + 4 y - 3 z - 12 = 0

Então vou começar por achar onde ele corta o eixo x : fazendo y = z = 0 temos:

6 x - 12 = 0

x = 12 6 = 2

Então o ponto é P 1 ( 2,0 , 0 ) .

Passo 3

Agora vamos achar onde esse plano corta o eixo y . Fazendo x = z = 0 na equação do plano temos:

4 y - 12 = 0

4 y = 12

y = 12 4 = 3

Assim o ponto onde esse plano corta o y é P 2 ( 0,3 , 0 ) .

Passo 4

Por fim precisamos achar onde esse plano corta o eixo z . Fazendo x = y = 0 na equação geral do plano temos:

- 3 z - 12 = 0

- 3 z = 12

z = 12 - 3 = - 4

O terceiro ponto é P 3 0 , 0 , - 4 .

Passo 5

Agora vamos ao desenho. Usando um programa de geração gráfica temos:

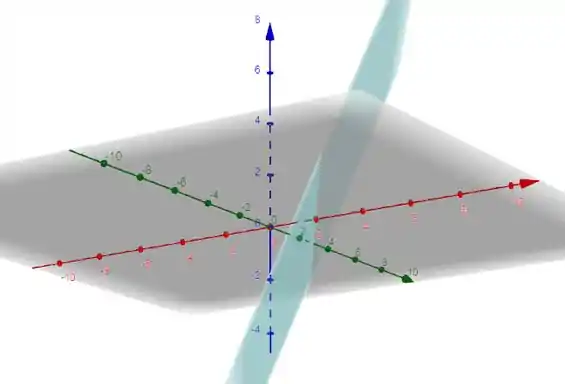
Notem que o ponto P 1 ( 2,0 , 0 ) está sob o eixo vermelho, o ponto P 2 ( 0,3 , 0 ) no eixo verde e P 3 ( 0,0 , - 4 ) no vermelho.

Espero ter ajudado!

Vamos pra próxima?

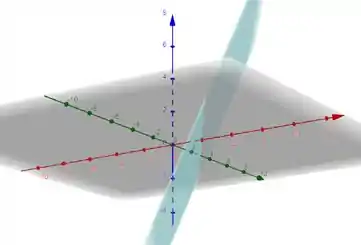
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Estude a posição relativa dos planos π 1 : 2 x + y + 3 z + 1 = 0 e π 2 : X = 1 ,1 ,1 + λ1 ,1 ,0 + μ( 2 ,- 1 ,m ) e verifique se existe algum valor de m para o qual π 1 e π 2 sejam perpendiculares.
Dados π 1 : X = 1 ,- 2 ,0 + λ1 ,0 ,- 1 + μ( 0 ,0 ,- 1 ) e π 2 : X = 1 ,0 ,3 + λ1 ,2 ,0 + μ( - 1 ,1 ,- 1 ) , obtenha uma equação vetorial de π 1 ∩ π 2 .
a) Prove que o lugar geométrico dos pontos de E 3 que equidistam de A = ( 1 ,- 1 ,2 ) e B = ( 4 ,3 ,1 ) é um plano.b) Prove que o plano do item (a) é perpendicular ao segmento A B e contém o seu ponto
Obtenha uma equção geral do plano que contém π 1 ∩ π 2 e é perpendicular a π 3 , sendo π 1 : x - y + z + 1 = 0 , π 2 : x + y - z - 1 = 0eπ 3 : x + y + 2 z - 2 = 0
Obtenha uma equação geral do plano π 1 que contém r : X = 1 ,0 ,1 + λ0 ,3 ,1 e é perpendicular a π 2 : x + y - 2 z - 2 = 0 , e obtenha uma equação vetorial de π 1 ∩ π 2 .