Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento algébrico - Ex. 36
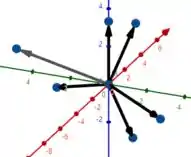
Representar no mesmo sistema o vetor com origem nos pontos , , , e .
Passo 1
Então galera, para calcularmos as coordenadas de um vetor nós realizamos a seguinte operação: vamos tomar um vetor qualquer , no qual é o ponto da extremidade e é o ponto referente à origem. Sendo assim, a operação é:
Em outras palavras:
O vetor e as origem já foram dadas pra gente, então:
E como temos origens diferentes, encontraremos extremidades! Let’s bora!
Passo 2
Para a origem :
Para a origem :
Para a origem :
Para a origem :
E, por fim, para a origem :
Passo 3
Agora que encontramos os vetores associados às origens diferentes, basta representarmos em um sistema de coordenadas cartesiano para vermos no que resulta. Plotando isso, teremos algo assim:
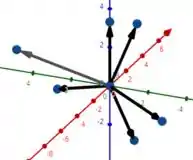
E assim fica a representação dos nossos novos vetores em apenas um sistema ! Espero que tenha ficado claro a ideia! 😉
Resposta
