Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento algébrico - Ex. 37
Sendo e vértices consecutivos de um paralelogramo e o ponto de intersecção das diagonais, determinar os vértices e .
Passo 1
Antes de iniciarmos a resolução propriamente dita, vamos esboçar esse paralelogramo , no qual é o ponto de intersecção das diagonais, se liga:
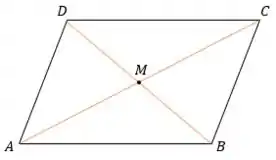
Caso você não se lembre, pela definição de paralelogramo nós temos que:
Ademais:
E essa conclusão também nos permite concluir que:
e
Show!
Passo 2
A primeira igualdade que escrevemos é:
Que também podemos escrever assim:
Substituindo os pontos e , obteremos:
Passo 3
A segunda igualdade que escrevemos é:
Que também podemos escrever assim:
Substituindo os pontos e , obteremos:
E esses são os vértices que queríamos encontrar!
Resposta
Vértices: e .
Exercícios de Livros Relacionados
1. A figura 1.29 apresenta o losango E F G H inscrito no retângulo A B C D , sendo O o ponto de intersecção das diagonais desse losango. Decidir se é verdadeira ou falsa cada uma das seguintes afirmaç
1. A figura 1.29 apresenta o losango E F G H inscrito no retângulo A B C D , sendo O o ponto de intersecção das diagonais desse losango. Decidir se é verdadeira ou falsa cada uma das seguintes afirmaç
2. Decidir se é verdadeira ou falsa cada uma das afirmações:c) Se u → / / v → , então u → = v → .
2. Decidir se é verdadeira ou falsa cada uma das afirmações:h) 5 v → = - 5 v → = 5 v → .
2. Dado os vetores u → = ( 3 ,- 1 ) e v → = - 1 ,2 , determinar o vetor x → tal que:b) 3 x → - 2 v → - u → = 2 4 x → - 3 u →