Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 16.Exercício - Ex. 13
A reta é paralela a , está contida em , e é concorrente com . Obtenha uma equação vetorial de , nos casos:
a)
b)
Passo 1
Antes de qualquer coisa, vamos analisar algumas informações:
- O plano tem vetor normal
- Como a reta é paralela a esse plano, o produto escalar do seu vetor diretor com é 0, pois eles serão perpendiculares:
Então já sabemos que o vetor diretor tem o formato né? Hahaha
- A reta está contida no plano , então, seu vetor diretor é paralelo a esse plano, e pela proposição 14-21:
Logo, o vetor diretor da nossa reta tem o formato hahaha boaa
Agora vamos lançar a braba fazendo a reta ser concorrente com a reta :P
Passo 2
a) Para que seja concorrente com , primeiramente, os seus vetores diretores devem ser LI.
Vamos ver qual o valor de que faz eles serem LD, e aí saberemos também que para os outros valores de eles vão ser LI hehe
Igualando as coordenadas:
A única solução desse sistema é , então, os vetores nunca vão ser LD, ou seja, vão ser LI para qualquer valor de !!
Passo 3
Como a reta está contida no plano, ela vai cruzar com no mesmo ponto onde cruza com o plano ok?
Então vamos encontrar a intersecção de com o plano. Um ponto genérico da reta é , substituindo na equação do plano:
Então, para , o ponto pertence a , ao plano e, consequentemente, à reta :
Passo 4
Logo, escolhendo , a reta pode ser escrita como:
Repare que para qualquer valor de que escolhermos, ele sempre será LD com , logo, independente do valor de , teremos a mesma reta ok?
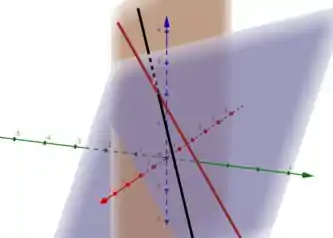
Abaixo temos em laranja o plano , em roxo o plano , em preto a reta e em vermelho a reta :) Repare que a reta está contida no plano, enquanto a reta é transversal a ele, portanto, com certeza a intersecção de com o plano seria a intersecção de com hehe
Passo 5
b) Para que seja concorrente com , primeiramente, os seus vetores diretores devem ser LI.
Vamos ver qual o valor de que faz eles serem LD, e aí saberemos também que para os outros valores de eles vão ser LI hehe
Igualando as coordenadas:
A única solução desse sistema é , então, os vetores nunca vão ser LD, ou seja, vão ser LI para qualquer valor de !!
Passo 6
Como a reta está contida no plano, ela vai cruzar com no mesmo ponto onde cruza com o plano ok?
Então vamos encontrar a intersecção de com o plano. Um ponto genérico da reta é , substituindo na equação do plano:
Então, para , o ponto pertence a , ao plano e, consequentemente, à reta :
Passo 7
Logo, escolhendo , a reta pode ser escrita como:
Repare que para qualquer valor de que escolhermos, ele sempre será LD com , logo, independente do valor de , teremos a mesma reta ok?
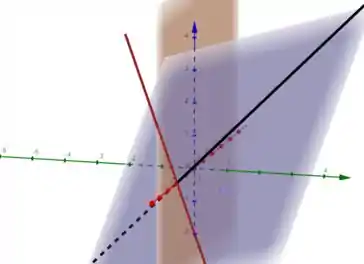
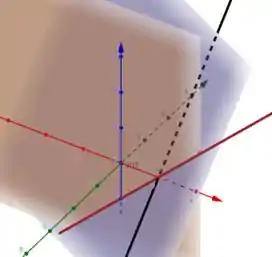
Abaixo temos em laranja o plano , em roxo o plano , em preto a reta e em vermelho a reta :) Repare que a reta está contida no plano, enquanto a reta é transversal a ele, portanto, com certeza a intersecção de com o plano seria a intersecção de com hehe
Repare também, que nesse caso a reta está contida também no plano , logo, ela é a intersecção dos dois planos :)
Resposta
a)
b)