Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 34
São dados, em cada caso, o foco e a diretriz de uma parábola. Obtenha uma equação algébrica de segundo grau em e que todo ponto da parábola deve satisfazer.
- ; .
- .
- .
Passo 1
Vamos lembrar da definição da parábola:
Uma parábola é o conjunto de pontos do plano tais que
Passo 2
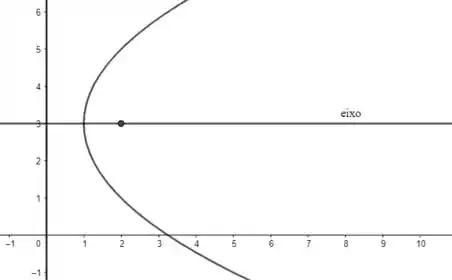
- Nesse caso, a diretriz é o eixo . O foco é . Assim, o eixo da parábola deve ser paralelo ao eixo (veja a figura). A distância de até deve ser igual a :
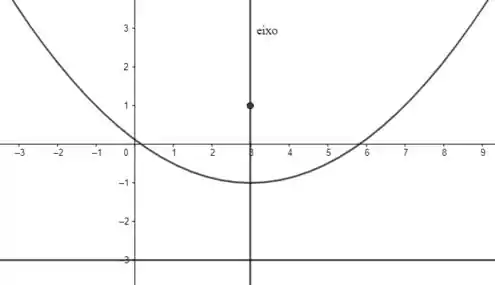
- A diretriz é , que é paralela ao eixo . O foco é , de modo que:
O vértice da parábola deve ser o ponto
Sua equação será:
Passo 3
O vértice será dado por:
E a equação:
Passo 3
Nesse caso, a diretriz é oblíqua aos eixos! Assim, os formatos das equações ou não valem mais, pois na dedução foi considerado que a diretriz era paralela a um dos eixos. Portanto, devemos apelar para a definição dada no Passo 1.
Seja, então um ponto da parábola.
A distância de até será:
A distância de até será:
Passo 4
Portanto,
Onde elevamos a equação ao quadrado. Desenvolvendo, temos
Observação: para expandir usamos o seguinte produto notável:
Resposta
Ei, a resposta está no passo a passo :)