Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 18.Exercício - Ex. 27a
Seja e . Nos casos do exercício anterior, obtenha equações do lugar geométrico dos pontos médios dos segmentos paralelos a com uma extremidade em e outra em . Descreva o lugar geométrico
(a)
Passo 1
(a) Bom pessoal, o primeiro passo aqui é relembrar bem rápido o que a gente tinha encontrado no exercício anterior.
Nós verificamos que o vetor normal do plano é:
Só pegando os coeficientes da equação de que o enunciado deu.
E que o vetor diretor da reta é:
Mas fazendo o produto escalar, olha o que acontece:
O produto escalar é nulo. Então os vetores são perpendiculares.
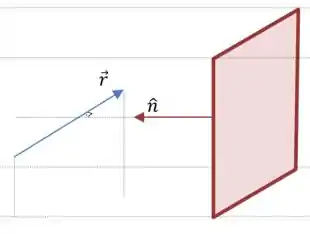
E se o vetor diretor da reta é perpendicular ao vetor normal do plano, então a reta é paralela ao plano.
Passo 2
Se a gente pegar os pontos médios de todos os segmentos que ligam a reta ao plano:
Eles vão formar um plano entre a reta e o plano. Como esse novo plano tem que ser paralelo a , a equação dele é:
Essa equação, conforme o varia, é a equação do feixe de planos paralelos a . Temos que ajustar para encontar nosso plano.
Para encontrar essa constate , a gente viu que, pela equação do enunciado, a reta começa em , então o plano que passa por essa reta seria:
E no plano temos . Como o novo plano deve estar entre esses dois:
Então o novo plano é:
Beleza, esse é um resumo do que foi feito.
Passo 3
E o que muda quando ao invés de pegar todos os segmentos entre e , nós só pegamos os que são paralelos a .
Vamos usar o desenho para entender. Quando estamos desenhando o plano, só vão sobrar os segmentos que são paralelos a :
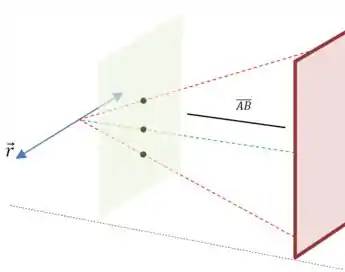
No desenho de cima, só sobraria o segmento pontilhado em verde. E os pontos médios dela continuam sobre aquele plano verde.
Quando pegarmos todas os segmentos paralelos a reta verde, vamos formar um plano:
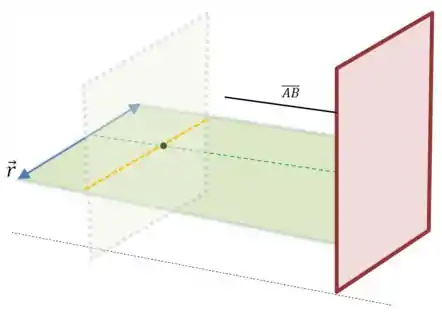
E o lugar geométrico formado pelo ponto médio é aquela reta pontilhada em laranja!
Passo 4
Dê mais uma olhada no desenho ali em cima.
Pra encontrar aquela reta pontilhada em laranja, a gente precisa procurar a equação geral daquele plano novo que está em verde.
A gente sabe que esse plano é paralelo à reta , que lá no enunciado tem esse vetor diretor aqui:
E também é paralela ao vetor , que também funciona como um vetor diretor:
E para completar tudo o que precisamos para fechar o plano, precisamos de um ponto qu esteja no plano. Podemos usar o ponto que está na equação vetorial da reta :
Agora é só lembrar do seguinte: se o vetor normal é e o ponto é , a equação geral do plano é:
Passo 5
Para encontrar o vetor normal, vamos fazer o produto vetorial dos dois vetores diretores:
Agora sim, dá pra achar a equação geral do plano:
Usando a fórmula lá de cima:
Então agora, pra terminar a questão, temos que achar a interseção entre esses plano e o que escrevemos lá em cima:
Passo 6
Isso é um sistema de duas equações que a gente pode resolver:
Já que temos três variáveis e duas equações, vai sobrar uma variável. Vamos deixar o como variável livre.
Então primeiro multiplicamos a equação de baixo por e somamos as duas:
E agora multiplicamos a equação de baixo por e somamos:
Ou seja, a interseção entre esses dois planos pode ser parametrizada desse jeito:
E passando isso para uma equação vetorial da nossa reta :
Pronto! Esse é o lugar geométrico que a gente estava procurando. Ele é a reta laranja naquele nosso desenho:
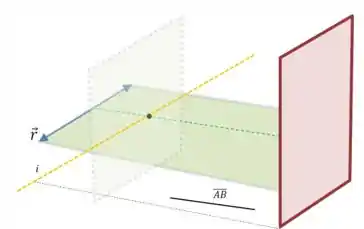
Resposta
O lugar geométrico é uma reta de equação vetorial . É a interseção do plano que encontramos no exercício anterior com o plano que contém a reta e é paralelo ao .