Seja e . Nos casos do exercício anterior, obtenha equações do lugar geométrico dos pontos médios dos segmentos paralelos a com uma extremidade em e outra em . Descreva o lugar geométrico

(b)

Quando temos essa situação, isso quer dizer que a reta é normal ao plano. Vamos ver como fica isso no desenho:

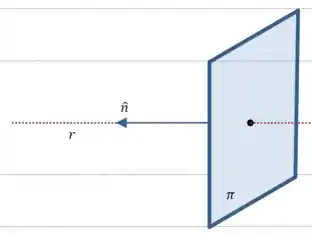
Ok, agora vamos ver como fica a álgebra da situação. Um ponto qualquer na reta é:

E para escrever um ponto qualquer no plano , precisamos da equação paramétrica do plano:

Então o ponto é:

Isso quer dizer que os segmentos entre a reta e o plano têm esse vetor diretor aqui:

Qual é a condição para esses segmentos serem paralelos ao segmento ?

E para que sejam paralelos:

Isso dá um sistema de três equações:

É um sistema de três equações e quatro incógnitas, então vai sobrar um grau de liberdade.

Vamos tentar escrever tudo em função de . Vamos subtrair a segunda equação da primeira:

E pela segunda equação:

Substituindo isso na última equação:

Substituindo isso no resultado de antes:

E para :

Então nossa solução é:

Agora vamos voltar nas equações dos pontos:

Os pontos que formam segmentos que são paralelos a são os que atendem à nossa solução:

Então:

E então os pontos médios entre os dois pontos:

Ou seja, essa reta contém os pontos médios dos segmentos entre a reta e o plano que são paralelos a .

Vamos chamar essa reta de :

Vamos demonstrar isso em um desenho:

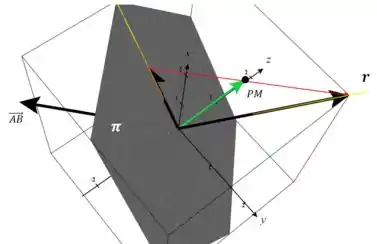
O desenho é um pouco confuso, mas vamos explicar.

Aquele vetor verde é o vetor diretor da reta que a gente encontrou na resposta.

O vetor vermelho é o “segmento” que liga a reta ao plano, e é paralelo ao vetor preto que está ali atrás.