Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Callioli - Álgebra Linear e Aplicações - Parte 1- Ed: 6º - Capítulo 4.4 - Ex. 14

Seja W = U ⊕ V . Consideremos os operadores lineares de W (projeções sobre U e V , respectivamente) dados por P 1 u + v = u e P 2 u + v = v , ∀ u + v ∈ W , com u ∈ U e v ∈ V . Definido por H : W → W por H w = P 1 w - P 2 w , ∀ w ∈ W , mostre que H é um isomorfismo do espaço vetorial W nele mesmo, isto é, H é um automorfismo de W .

Tome W = R 2 , U = 1,1 , , V = 1 , - 1 e represente geometricamente U , V , W , P 1 , P 2 , H .

Passo 1

Esta questão nós podemos dividir em duas partes. A primeira é uma parte teórica, que precisamos provar que H é um automorfismo. Já a segunda é um estudo de caso. Temos que representar os subespaços no R 2 .

Então, vamos começar pela primeira parte. Provar que H é um automorfismo é verificar que o núcleo da sua transformação possui apenas o vetor nulo. Mas, para isto, temos que saber quem é H primeiro. Ele será dado por:

H w = P 1 w - P 2 w

H w = P 1 u + v - P 2 u + v

H w = u - v

Sendo w = u + v .

Passo 2

Agora, vamos descobrir quem é o vetor w = u + v que pertença ao núcleo de H . Para isto, o vetor tem que satisfazer a seguinte relação: H w = 0 . Portanto,

H w = 0

H w = u - v = 0

A vontade que temos é fazer:

u - v = 0 ⟹ u = v

Essa é uma vontade grande, dizer que basta que u seja v para qualquer v . Entretanto, não podemos fazer isto, pois u e v pertencem a subespaços vetoriais distintos! A única solução em comum, a qual é a solução da equação acima, é u = v = 0 , isto é, ambos são os vetores nulos

Portanto, o único vetor w que pertence ao núcleo é o vetor nulo. Logo, dim ⁡ ker ⁡ H = 0 , e assim, verificamos que H é injetora e, consequentemente, um automorfismo!

Passo 3

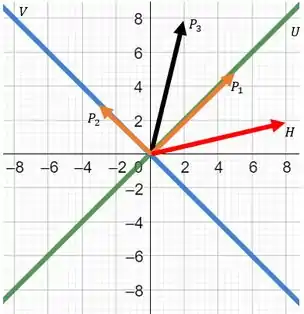
Agora temos que fazer um estudo de caso. O nosso espaço W é o R 2 , e os subespaços U e V possuem as seguintes bases: U = 1,1 e V = 1 , - 1 .

Para desenharmos geometricamente os subespaços no plano O x y (o qual é o espaço W ), vamos desenhar retas que representam cada um dos espaços que estamos trabalhando.

O espaço U é a reta que forma uma inclinação de 45° com o eixo O x (vetor u = 1,1 ). O espaço V é a reta que forma uma inclinação de -45° com o eixo O x (vetor v = 1 , - 1 )

As operações P 1 e P 2 são as projeções de um vetor w qualquer em cada uma das retas que representam U e V . Por fim, temos a aplicação H , a qual corresponde a uma rotação do vetor w .

Se esboçarmos todas estas relações no plano O x y , teremos:

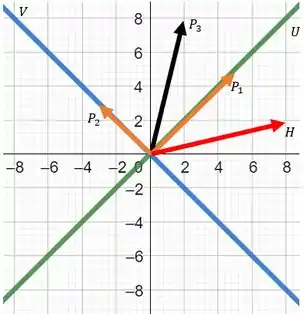
Resposta

Prova-se que H é um automorfismo verificando que o seu núcleo é igual ao conjunto vazio.

A representação dos subespaços U , V , W , P 1 , P 2 e H dado um vetor w qualquer é:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada parte, use a informação dada para determinar se a transformação linear T é injetora. T : R m → R m ; n u l T = 0 . T : R n → R n : p o s T = n - 1 . T : R m → R n ; nm . T : R n → R n ; R T =
Conforme indicado na figura, seja T : R 2 → R 2 o operador linear que reflete cada ponto no eixo y .Encontre o núcleo de T . T será injetora? Justifique sua resposta.
Quais das transformações do Exercício 1 são sobre. T : R 2 → R 2 , com T x ,y = ( y ,x ) . T : R 2 → R 2 , com T x ,y = ( 0 ,2 x + 3 y ) . T : R 2 → R 2 , com T x ,y = ( x + y ,x - y ) . T : R 2 → R 3
Seja T : V → V um operador linear. Prove que T é injetor se, e só se, det ⁡ T ≠ 0
(Requer Cálculo) Seja J : P 1 → R a transformação de integração J p = ∫ - 1 1 p x d x . Determine se J é injetora. Justifique sua resposta.