Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 139

Seja X = x ,   y um ponto da elipse E : x 2 / a 2 + y 2 / b 2   = 1 , de focos F 1 e F 2 e excentricidade e .

  1. Mostre que X F 1 → ⋅ X F 2 → = e 2 x 2 + a 2 1 - 2 e 2 .
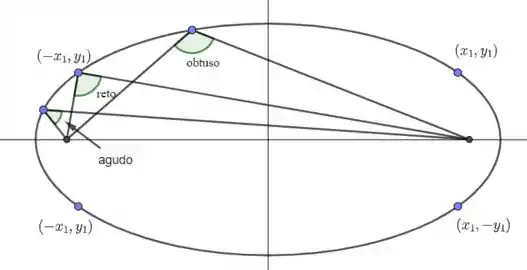
  2. Analisando o sinal de X F 1 → ⋅ X F 2 → em função dos valores de e , estude a natureza do ângulo (reto, agudo, obtuso) sob o qual o ponto X vê o segmento focal (esta linguagem é usual em Geometria: trata-se do ângulo F 1 X ^ F 2 ).

Passo 1

  1. Sejam F 1 = - c ,   0 e F 2 = c ,   0 . Como X ∈ E , segue que se X = x ,   y , então:

    x 2 a 2 + y 2 b 2 = 1 ⟹ y 2 = b 2 - b 2 a 2 x 2

    Vamos calcular X F 1 → e X F 2 → :

    X F 1 → = F 1 - X = - c ,   0 - x ,   y = - c - x ,   - y

    X F 2 → = F 2 - X = c ,   0 - x ,   y = c - x ,   y

    Portanto:

    X F 1 → ⋅ X F 2 → = - c - x ,   y ⋅ c - x ,   y = - c + x ⋅ c - x + y 2

    X F 1 → ⋅ X F 2 → = - c 2 - x 2 + y 2 = x 2 + y 2 - c 2

    X F 1 → ⋅ X F 2 → = x 2 + b 2 - b 2 a 2 x 2 - c 2

    X F 1 → ⋅ X F 2 → = x 2 1 - b 2 a 2 + b 2 - c 2

    Como a 2 = b 2 + c 2 , segue que

    X F 1 → ⋅ X F 2 → = x 2 c 2 a 2 + b 2 - c 2 = x 2 e 2 + a 2 - 2 c 2

    X F 1 → ⋅ X F 2 → = x 2 e 2 + a 2 1 - 2 c a 2 = x 2 e 2 + a 2 1 - 2 e 2

    ∴ X F 1 → ⋅ X F 2 → = x 2 e 2 + a 2 1 - 2 e 2

    Como queríamos demonstrar!

    Passo 2

Vamos dividir em casos:

  1. O ângulo é agudo:

    2. ∴ X F 1 → ⋅ X F 2 → > 0 ⟹ x 2 e 2 + a 2 1 - 2 e 2 > 0

    Veja que isso acontecerá sempre, desde que 1 - 2 e 2 > 0 ∴ 2 e 2 < 1 ∴ e < 2 / 2 .

    Portanto, sempre que 0 < e < 2 / 2 , qualquer ponto da elipse vê o segmento focal com um ângulo agudo!

  2. O ângulo é reto:

∴ X F 1 → ⋅ X F 2 → = 0 ⟹ x 2 e 2 + a 2 1 - 2 e 2 = 0

Agora, note que se e = 2 / 2 , então x 2 e 2 = 0 ⟹ x = 0 , ou seja, os pontos de abscissa 0 irão enxergar o segmento focal com ângulo reto; os pontos que possuem abscissas nula são B 1 e B 2 .

Por outro lado, se 2 / 2 < e < 1 , sejam x 1 e x 2 as raízes da equação

x 2 e 2 + a 2 1 - 2 e 2 = 0

Passo 2

Assim, existem exatamente quatro pontos P = x 1 ,   y 1 ,   Q = x 1 ,   - y 1 , R = - x 1 ,   y 1 , S = - x 1 , - y 2 que enxergam o segmento focal com ângulo reto. Os pontos com abscissas x < x 1 irão enxergar o segmento focal com ângulo obtuso e os pontos com abscissas x > x 1 irão enxergar a elipse com ângulo agudo.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache o centro, vértices, focos, extremidade do eixo menor da elipse dada. Faça um esboço da curva, mostrando os focos. 3 x 2 + 4 y 2 = 9
Ache o centro, vértices, focos, extremidade do eixo menor da elipse dada. Faça um esboço da curva, mostrando os focos. 64 x 2 + y 2 = 16
Ache o centro, vértices, focos, extremidade do eixo menor da elipse dada. Faça um esboço da curva, mostrando os focos. 3 x 2 + 4 y 2 - 30 x + 16 y + 100 = 0
Ache o centro, vértices, focos, extremidade do eixo menor da elipse dada. Faça um esboço da curva, mostrando os focos. 2 x 2 + 3 y 2 - 4 x + 12 y + 2 = 0
Ache o centro, vértices, focos, extremidade do eixo menor da elipse dada. Faça um esboço da curva, mostrando os focos. 6 x 2 + 9 y 2 - 24 x - 54 y + 51 = 0