Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 37.Problemas - Ex. 5

Seja M: R 2 → R 2 a transformação linear definida por M ( x , y ) =   ( a 1 x + b 1 y ,   a 2 x + b 2 y ) . Se a matrizes m = a 1 b 1 a 2 b 2 é não-nula e d e t   m = 0 , a imagem de M é uma reta passando pela origem. Se d e t m ≠ 0 ,   prove que M transforma todo triângulo O A B   num triângulo O A ’ B ’ tal que ( á r e a   d e   O A ’ B ’ ) =   | d e t m | .   Á r e a   d e   O A B . Prove que o esmo fato vale para triângulos nos quais a origem não é um vértice.

Passo 1

Fala galerinha , vamos resolver mais uma questão do nosso livro de Geometria analítica e Álgebra Linear !!!

Vamos começar montando as duas matrizes solicitas na questão. Uma matriz m ’ com determinante igual a zero e outra matriz m ’ ’ com determinante diferente de zero.

Lembrando que uma matriz nula é aquela cuja todos os elementos que compõem a matriz é igual a zero e que independe da quantidade de linhas ou colunas. Logo, uma matriz não-nula será,

m ' = a 1 b 1 0 0

E com um determinante equivalente a d e t   m ’ = 0 . E,

m ' ' = a 1 b 1 0 b 2

com um determinante equivalente a d e t   m ’ ’ = a 1 . b 2

Galera, vamos para o próximo passo e prova as situações dadas na questão.

Passo 2

O próximo passo é lembra que um conjunto de imagem de uma determinada função é igual aos valores encontrados, ou seja, os resultados.

Vamos primeiro realizar a análise para matriz m’

m ' = a 1 b 1 0 0

Logo realizando a transformação proposta na questão é encontrado para os pontos ( a 1,0 ) e ( b 1,0 ) que,

M ( x , y ) =   ( a 1 x + b 1 y ,   0 )

E se a reta passa pela origem o resultado da função de M x , y = ( 0,0 ) .

M x , y = a 1 x + b 1 y ,   0 = 0,0

a 1 x + b 1 y = 0

a 1 x = - b 1 y

Passo 3

Vamos encontrar agora o d e t   m ' ' ≠ 0 .

m ' ' = a 1 b 1 0 b 2

Logo, realizando a transformação proposta na questão é encontrado os pontos a 1,0 e b 1 , b 2 da matriz m ’ ’

M ( x , y ) =   ( a 1 x + b 1 y ,   b 2 y )

Na questão é solicitado analisar a transformação para situação onde se precisa encontrar o valor da área de um triângulo.

Assim, vamos propor um triângulo equilátero, ou seja, cujas suas arestas possui o mesmo módulo e suas vértices serão,

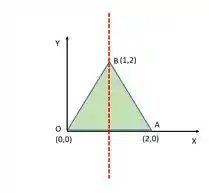
Lembrando que a área do triângulo é dado por,

á r e a   O A B = O A . H 2

Sendo H o valor da altura do triângulo.

Para calcular o valor da área do triângulo vamos primeiro calcular o valor das transformações para cada vértices,

M ( x , y ) =   ( a 1 x + b 1 y ,   b 2 y )

M ( 0 , 0 ) =   ( a 1 . 0 + b 1 . 0 ,   b 2 . 0 )

M ( 0 , 0 ) =   ( 0 ,   0 )

M ( 2 , 0 ) =   ( a 1 . 2 + b 1 . 0 ,   b 2 . 0 )

M ( 2 , 0 ) =   ( 2 a 1 ,   0 )

M ( 1 , 2 ) =   ( a 1 . 1 + b 1 . 2 ,   b 2 . 2 )

M ( 1 , 2 ) =   ( a 1 + 2 b 1 ,   2 b 2 )

E para o valor da altura H transformação será,

M ( 0 , 2 ) =   ( a 1 . 0 + b 1 . 2 ,   b 2 . 2 )

M ( 0 , 2 ) =   ( 2 b 1 ,   2 b 2 )

Logo a de á r e a   O A B ,

á r e a   O A B = O A . H 2 = M ( 2,0 ) . M ( 0,2 ) 2

á r e a   O A B = ( a 1 . 2 + b 1 . 0 ,   b 2 . 0 ) . ( 2 b 1 ,   2 b 2 ) 2

á r e a   O A B = ( 4 a 1 . b 1 + 2 b 1 2 ,   2 b 2 2 ) 2

á r e a   O A B = ( 2 a 1 . b 1 + b 1 2 ,   b 2 2 )

Passo 4

Agora vamos calcular a de á r e a   d e   O A ’ B ' =   | d e t m | .   Á r e a   d e   O A B

á r e a   O A ’ B ' =   d e t m ' ' .   Á r e a   d e   O A B

á r e a   O A ’ B ' = ( a 1 . b 2 ) . ( 2 a 1 . b 1 + b 1 2 ,   b 2 2 )

á r e a   O A ’ B ' = ( 2 a 1 2 . b 2 . b 1 + a 1 . b 2   b 1 2 ,   a 1 . b 2 3 )

Resposta

Então, podemos concluir os valores dos coeficientes das matrizes e como também a relação de transformação para cada uma das situações ( d e t   = 0   e   d e t ≠ 0 )

Espero que ajudem nos estudos, até próxima

Exercícios de Livros Relacionados

Quantas inversões tem a permutação ( n n - 1 ... 2 1 ) dos números 1 , 2 , ... , n - 1 , n ?
Calcule det A , ondeA = |[[3,-,1,5,0],[0,2,0,1],[2,0,-,1,3],[1,1,2,0]]| |[[3,0,0,0,0],[19,18,0,0,0],[-,6,pi,-,5,0,0],[4,sqrt(2),sqrt(3),0,0],[8,3,5,6,-,1]]| |[[i,3,2,-,i],[3,-,i,1,i],[2,1,-,1,0],[-,i,
A partir do exercício acima, você pode concluir que uma matriz A , de ordem n , possui determinante diferente de zero se, e somente se A tem n linhas linearmente independentes. Por quê? (Veja o final
Dado um polinômio p ( t ) = ( - 1 ) n ( t n + a n - 1 t n - 1 + ⋯ + a 0 ) Verifique que a matriz ⎜01 0⋯0 ⎜⎜ ⎜ ⎜00 1⋯0 ⎜⎜ ⎜ ⎜ ⋯ ⋯⋯ ⋯⋯ ⎜⎜ ⎜ ⎜00 0⋯1 ⎜⎜ ⎜ ⎜ - a 0- a 1- a 2 ⋯- a n - 1⎜⎜ ⎜é tal que d e t (
Responda Verdadeiro ou Falso, justificando:(a) Se A 2 = - 2 A 4 , então I + A 2 - 1 = I - 2 A 2 ;(b) Se A t = - A 2 e é não singular, então determinante de A é - 1 ;(c) Se B = A A t A - 1 , então d e