Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 24.Exercício - Ex. 19
Sejam e . Determine , em cada caso:
é tangente a
é secante a
é exterior a
Passo 1
Primeiramente vamos encontrar a equação reduzida da esfera, primeiramente dividindo tudo por 8:
Isso nos dá:
E uma forma de completar esses quadrados é:
Não se esquecendo que o que formos somar de um lado tem que somar do outro.
O que nos dá:
Passo 2
E a nossa reta tem uma equação que segue uma equação igual a:
Aplicando esse ponto na equação da esfera nós iremos obter:
E abrindo essa equação e colocando tudo em função de nós iremos ter:
Passo 3
Ai aqui que começa questão pois para termos uma reta secante nós devemos fazer , pois essa reta somente terá um valor de inclinação que tangenciará a esfera.
Cujas raízes são e , como não teremos reta em então é a única solução viável.
Passo 4
Agora para secante nós devemos fazer , ou seja:
Onde essa equação pode ser simplificada para:
E esse valor simplesmente não existe, pois nos dá um valor zero para essa equação, todos os valores de nos dão um valor menor que zero.
Agora para exterior basta termos e para isso temos todos os valores de menos e
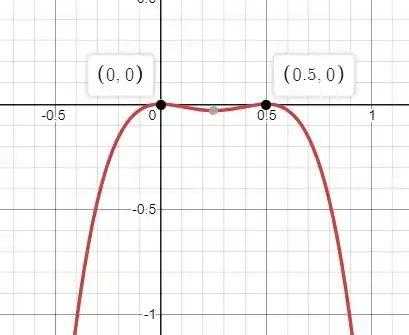
Gráfico de