Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 14.Exercício - Ex. 10
Sejam , e .
a) Mostre que e são vértices de um triângulo.
b) Escreva equações paramétricas da reta que contém a mediana relativa ao vértice .
Passo 1
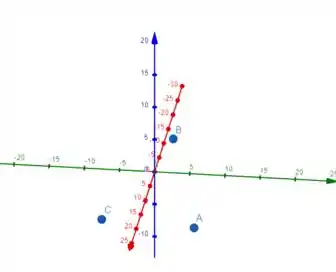
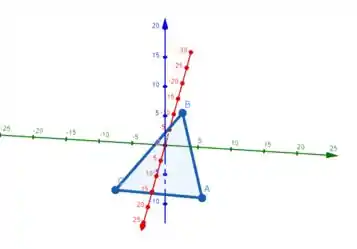
a) Para que esses pontos sejam vértices de um triângulo, eles não devem ser colineares, ou seja, não pode ser paralelo a , por exemplo.
Temos:
Podemos notar que e não são paralelos, pois um não é múltiplo do outro certo?
Então, os 3 pontos não são colineares e aí formam um triângulo ;)
Passo 2
b) A reta que determina essa mediana vai passar pelo ponto médio do segmento e vai ter vetor diretor beleza?
Primeiro, vamos encontrar :
Passo 3
Agora o vetor :
E assim, temos a equação da reta que determina a mediana relativa ao vértice :
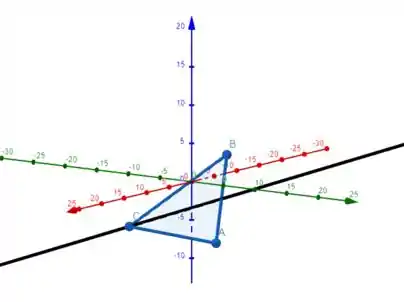
Resposta
b)
Exercícios de Livros Relacionados
Obtenha o ponto simétrico do ponto P em relação à reta r , nos casos: P = 0 ,2 ,1 r : X = 1 ,0 ,0 + λ( 0 ,1 ,- 1 )
A diagonal B C de um quadrado A B C D está contida na reta r : X = 1 ,0 ,0 + λ( 0 ,1 ,1 ) . Conhecendo A = ( 1 ,1 ,0 ) , determine os outros três vértices.
Obtenha o ponto simétrico do ponto P em relação à reta r , nos casos: P = 0 ,0 ,- 1 r : x - y - z = 0 = 2 x + 3 y - 1
Estude a posição relativa das retas r e s g) r : x + 1 2 = y = - z s :x + y - 3 z = 1 2 x - y - 2 z = 0
Estude a posição relativa das retas r e s e) r : X = 8 ,1 ,9 + λ 2 ,- 1 ,3s :X = 3 ,- 4 ,4 + λ ( 1 ,- 2 ,2 )