Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 14.Exercício - Ex. 12
Sejam, em relação a um sistema ortogonal, e . Verifique que esses pontos são vértices de um triângulo e escreva uma equação vetorial da reta que contém a altura relativa ao vértice .
Passo 1
Para que esses pontos sejam vértices de um triângulo, eles não devem ser colineares, ou seja, não pode ser paralelo a , por exemplo.
Temos:
Podemos notar que e não são paralelos, pois um não é múltiplo do outro certo?
Então, os 3 pontos não são colineares e aí formam um triângulo ;)
Passo 2
A reta que contém a altura do triângulo relativa ao vértice deve ser perpendicular à reta que contém o segmento , ou seja, o vetor diretor de deve ser perpendicular a .
Primeiro vamos encontrar a reta que contém :
Sabendo que :
Passo 3
Seja o ponto de intersecção da reta com a reta . O vetor diretor de será .
Como também pertence à reta , que já temos a equação, ele pode ser escrito como:
Então será:
Passo 4
Sabemos que deve ser perpendicular a , então:
Opaa, descobrimos que pra ser perpendicular a (e portanto, representar a altura do triângulo relativa ao vértice ), o valor de deve ser :P
Passo 5
Então, a equação da reta , sabendo que ela passa pelo ponto e que seu vetor diretor é , vai ser:
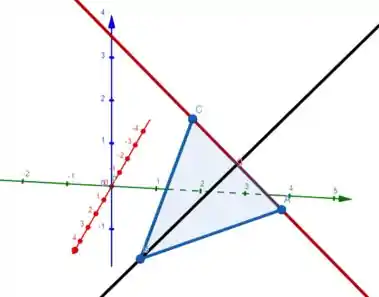
Nessa figura abaixo a reta preta é e a vermelha é :)
