Sejam e , respectivamente, vetores diretores das retas e . Mostre que um plano forma ângulos congruentes com essas retas se, e somente se, os comprimentos das projeções ortogonais de cada vetor normal a sobre e são iguais.

Seja o plano com seu vetor normal como mostrado abaixo

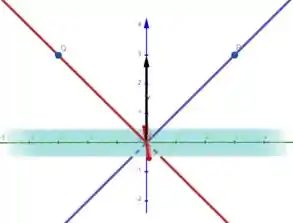
Vamos acrescentar retas genéricas, assim:

A projeção do vetor normal do plano é dada assim:

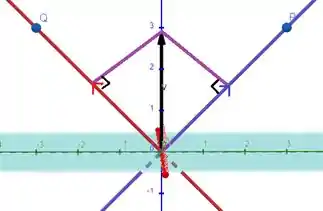
O que nos dá dois triângulos congruentes, na parte superior e na parte inferior ao ângulo de .

Por congruência de triângulos, se o vetor vermelho e o vetor azul (lados do triângulo) tiverem módulos iguais, o vetor normal terá ângulos congruentes com os dois.

Assim como se o vetor normal tiver ângulos congruentes com os dois, os vetores terão módulos iguais, sacou? Hahaha