Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 7.Exercício - Ex. 12

No tetraedro A B C D , seja X um ponto tal que   A X → = m   X D → . Determine os valores de m para os quais os vetores   A X → + A C → ,   B X → + B C → e 1 - m   B C → + A B → sejam LD.

Passo 1

Aqui, a primeira coisa que você precisa fazer é imaginar o tetraedro e fazer um esboço, marcando o ponto X entre A e D :

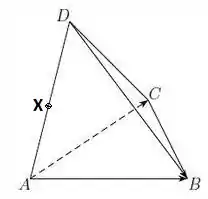
Feito isso, vamos escolher uma base para trabalhar (afinal, o capítulo é sobre bases né). Vou escolher a base E = A B → ,   A C → ,   A D → , que dão origem ao tetraedro.

Passo 2

O que temos que fazer agora é escrever cada um dos vetores u → = A X → + A C → , v → = B X → + B C → e w → = 1 - m   B C → + A B → na base E .

Note que

A X → = A D → + D X → = A D → - X D → = A D → - 1 m   A X →

Multiplicando a equação por m :

m   A X → = m   A D → - A X → ⇒ m + 1   A X → = m   A D → ⇒ A X → = m m + 1   A D →

Portanto,

u → = A X → + A C → = m m + 1   A D → + A C → = 0 ,   1 , m m + 1 E

Passo 3

Agora vamos olhar para v → = B X → + B C → :

B X → = B A → + A X → = - A B → + m m + 1   A D → =

B C → = B A → + A C → = - A B → + A C →

Assim,

v → = - 2   A B → + A C → + m m + 1   A D → = - 2 ,   1 , m m + 1 E

Por fim, para w → = 1 - m   B C → + A B → :

w → = 1 - m   - A B → + A C → + A B → = m   A B → + 1 - m   A C → = m ,   1 - m ,   0 E  

Passo 4

Para que os vetores sejam LD, o determinante com as coodernadas deve ser zero:

0 1 m m + 1 - 2 1 m m + 1 m 1 - m 0 = 0

Desenvolvendo com relação a primeira linha:

- 0 - m 2 m + 1 + m m + 1 - 2 + 2 m - m = 0

Assim,

m 2 m + 1 + m ( m - 2 ) m + 1 = 0

Usando que m ≠ - 1 , simplificamos a equação para

m 2 + m 2 - 2 m = 0 ⇒ m 2 - m = 0 ⇒ m m - 1 = 0

Portanto,

m = 0           o u           m = 1

Resposta

m = 0             o u           m = 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quais dos conjuntos de vetores dados são bases de P 2 ?d) - 4 +x +3 x 2 ,6 +5 x +2 x 2 ,8 +4 x+x 2
Quais dos conjuntos de vetores dados são bases de R 3 ?a) u 1 =1 ,0 ,0 ,u 2 =2 ,2 ,0 ,u 3 = ( 3 ,3 ,3 )
Quais dos conjuntos de vetores dados são bases de P 2 ?c) 1 +x +x 2 ,x +x 2 ,x 2
Mostre que as matrizes dadas formam uma base de M_22 .A = [[[3,6],[3,-,6]]] , B = [[[0,-,1],[-,1,0]]] , C = [[[0,-,8],[-,12,-,4]]] , D = [[[1,0],[-,1,2]]]
Em cada parte, explique em palavras por que os vetores dados não são uma base do espaço vetorial dado.c) p 1 =1 +x +x 2 ,p 2 =x -1p a r aP 2