Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 15.Exercício - Ex. 15
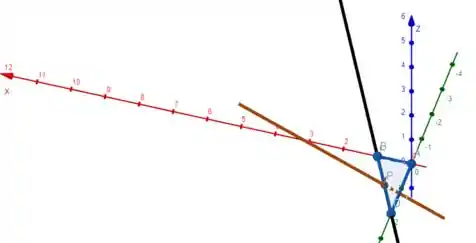
Um triângulo retângulo de área 1 tem os catetos contidos nos eixos e e a hipotenusa na reta . Seus vértices têm coordenadas inteiras, e é concorrente com a reta
Escreva uma equação vetorial de (o sistema de coordenadas é ortogonal).
Passo 1
Temos algo desse tipo aqui:
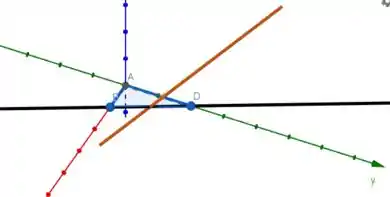
Onde a reta laranja é a reta e a reta preta é , que não conhecemos.
Passo 2
Antes de qualquer coisa, vamos encontrar a reta , ela é a intersecção entre os planos:
Multiplicando a equação de baixo por :
Somando as duas equações:
Substituindo na equação de cima:
Então, a reta é dada por
Trocando o parâmetro por , temos
Passo 3
Agora vamos analisar duas informações aqui:
O enunciado disse que o triângulo retângulo tem área , ou seja:
Mas ao mesmo tempo, ele disse que as coordenadas dos vértices são inteiras.
Então, ou e ou e .
Dessa forma, temos duas opções para os vértices e catetos desse triângulo retângulo:
e
e
Dessa forma, a princípio teríamos duas opções pra reta :
Passo 4
O enunciado nos disse que a reta é concorrente com a reta , ou seja, elas devem se cruzar em algum momento.
Como a reta está no plano , ou seja, no plano , a reta vai cruzar com a reta no mesmo ponto onde cruza esse plano:
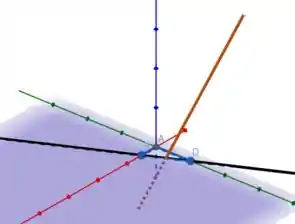
Vamos encontrar a intersecção da reta com o plano .
Um ponto genérico da reta é
Vamos substituir esse ponto no plano:
Opa, então a intersecção da reta e do plano é dada quando , ou seja:
Que é o mesmo ponto onde a reta vai cruzar a reta :D
Passo 5
Vimos no passo 3 duas opções para a reta :
Mas agora temos que conferir em qual delas vai passar o ponto , para que assim, elas sejam concorrentes com a reta .
Vamos lá, primeiro para a reta :
Igualando as coordenadas:
Da segunda equação, temos que . Substituindo na primeira:
Opa, chegamos em uma desigualdade, então não existe tal que pertença à reta :/ Então ela não é concorrente com a reta .
Passo 6
Agora vamos testar para a reta :
Da segunda equação, temos . Substituindo na primeira equação:
Ebaaa, então esse sistema é possível e existe um tal que pertença a !!
Então é a reta que estávamos procurando:
E vimos no passo 3 que ela é dada quando e :
