Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Posição relativa entre planos

Ver Todos os Exercícios

Teoria

Fala aí! Você está no Responde Aí! E agora vamos entender tudo sobre posição relativa entre planos.

A gente já viu como lidar com posição relativa entre retas e com a posição relativa entre reta e plano (caso não tenha visto, é só clicar nos links). Então a última parte do assunto é estudar a posição relativa entre planos.

Tipos de posição relativa entre planos

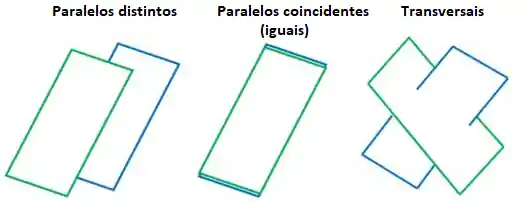
Quando tratamos de dois planos há três tipos de posições relativas possíveis:

  1. Paralelos distintos: os planos nunca se tocam!
  2. Paralelos coincidentes (iguais): Um plano está perfeitamente em cima do outro. Na prática, são equações diferentes para representar um mesmo plano.
  3. Transversais: Os planos estão se cruzando!
Posições relativas entre planos
Posições relativas entre planos

Como determinar a posição relativa entre os planos?

Vamos imaginar dois planos e , que a gente pode representar assim:

Para determinar a posição relativa entre dois planos precisamos comparar os coeficientes , , e dos planos.

  • Os planos são paralelos coincidentes quando os quatro coeficientes são proporcionais entre si:
  • Os planos são paralelos distintos quando os coeficientes , e são proporcionais entre si e o coeficiente não é
  • Planos são transversais quando pelo menos um dos coeficiente , e não é proporcional

Exemplo

Vamos ver um exemplo. Qual é a posição relativa entre os planos e

Primeiro, vamos separar as posições do plano

Para que eles sejam paralelos deve a equação abaixo deve ser verdade:

Abrindo essa equação vamos ter:

E agora a gente analisa. Observe que os coeficientes , e são proporcionais entre si com um fator de . Porém, o coeficiente não segue essa regra. Resultado: são planos são paralelos distintos.

Planos perpendiculares.

Um caso especial é quando dois planos formam entre si, isso é chamado de planos perpendiculares.

Para analisar se a posição relativa entre planos é perpendicular devemos olhar para o vetor normal de cada plano.

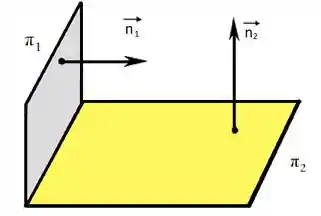
Planos perpendiculares e vetores normais
Planos perpendiculares e vetores normais

Dois planos são perpendiculares se o produto interno entre os vetores normais dos planos for ZERO.

Pra não ficar perdido, da uma olhada nesse super resumo:

Resumo:

Tipos de Posição Relativa de Planos

⇒ Paralelos distintos, Paralelos coincidentes, Transversais

⇒ Dado os planos:

  • Se → Paralelos coincidentes
  • Se → Paralelos distintos
  • Se → Transversais

E da uma olhada nesse super vídeo também!

Gostou?! Então continua que aqui em baixa tem um monte de exercícios pra você praticar 👇

Como determinar a posição relativa entre os planos?

Planos perpendiculares.

Resumo:

Exercícios Resolvidos

Exercício Resolvido #1

Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 185-1.

Estude a posição relativa de π 1 e π 2 nos seguintes casos:

  1. π 1 : X = 1 ,   1 ,   1 + λ 0 ,   1 ,   1 + µ - 1 ,   2 ,   1

      π 2 : X = 1 ,   0 ,   0 + λ 1 ,   - 1 ,   0 + µ - 1 ,   - 1 ,   - 2

  2. π 1 : 2 x - y + 2 z - 1 = 0

    π 2 : 4 x - 2 y + 4 z = 0

π 1 : x - y + 2 z - 2 = 0

π 2 : X = 0 ,   0 ,   1 + λ 1 ,   0 ,   3 + µ - 1 ,   1 ,   1

Passo 1

Bora estudar a posição relativa entre planos?!! Vamos nessa, então!!

O enunciado nos dá a equação vetorial dos planos. Mas, aprendemos a ver a posição relativa entre os planos por meio dos coeficientes da equação geral. Então, primeiro teremos que achar a equação geral de cada plano, para depois compararmos os coeficientes.

Passo 2

a Antes de achar as equações gerais dos planos, vamos retirar os dados:

π 1 : A = ( 1 ,   1 ,   1 ) v → = ( 0 ,   1 ,   1 ) u → = ( - 1 ,   2 ,   1 )           e                   π 2 : B = ( 1 ,   0 ,   0 ) r → = ( 1 ,   - 1 ,   0 ) s → = ( - 1 ,   - 1 ,   - 2 )

Montando e resolvendo o produto misto para achar a equação geral de cada plano temos:

Para   π 1 :

- x - y + z + 1 = 0

x + y - z - 1 = 0

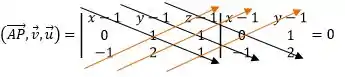
Para   π 2 :

2 x + 2 y - 2 z - 2 = 0

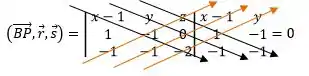
Agora, que temos todos os coeficientes podemos comparar os planos:

π 1 :     a 1 ,   b 1 , c 1 , d 1 = ( 1 ,   1 ,   - 1 ,   - 1 )

π 2 :   a 2 ,   b 2 , c 2 , d 2 = ( 2 ,   2 ,   - 2 ,   - 2 )

Se   (   a 1 ,   b 1 , c 1 , d 1 ) = α ( a 2 ,   b 2 , c 2 , d 2 ) então os planos são paralelos coincidentes. E, pelos coeficientes que temos:

1 ,   1 ,   - 1 ,   - 1 = 1 2 ( 2 ,   2 ,   - 2 ,   - 2 )

Portanto, os planos são paralelos coincidentes.

Passo 3

b

π 1 : 2 x - y + 2 z - 1 = 0

π 2 : 4 x - 2 y + 4 z = 0

O enunciado já nos dá a equação geral dos planos. Ufa!!! Menos contas!!

Temos que:

π 1 :     a 1 ,   b 1 , c 1 , d 1 = ( 2 ,   - 1 ,   2 ,   - 1 )

π 2 :   a 2 ,   b 2 , c 2 , d 2 = ( 4 ,   - 2 ,   4 ,   0 )

Bora comparar os coeficientes!!

Comparando percebemos que:

a 1 ,   b 1 , c 1 = 1 2 ( a 2 ,   b 2 , c 2 )

2 ,   - 1 ,   2 = 1 2 ( 4 ,   - 2 ,   4 )

Já os coeficientes d 1 e d 2 não são proporcionais. Assim, os planos são paralelos distintos.

Passo 4

c

π 1 : x - y + 2 z - 2 = 0

π 2 : X = 0 ,   0 ,   1 + λ 1 ,   0 ,   3 + µ - 1 ,   1 ,   1

Esse item é uma mistura entre os itens a e b . Pois, do plano π 1 foi nos dada a equação geral, já do plano     π 2 temos a equação vetorial. Assim, antes de fazermos qualquer análise teremos que encontrar primeiro a equação geral do plano     π 2 .

Montando e resolvendo o produto misto, temos:

A = 0,0 , 1 ,   v → = 1 ,   0 ,   3 ,   u → = - 1 ,   1 ,   1

- 3 x - 4 y + z - 1 = 0

3 x + 4 y - z + 1 = 0

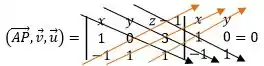
Já que temos todos os coeficientes, basta compararmos:

π 1 :     a 1 ,   b 1 , c 1 , d 1 = ( 1 ,   - 1 ,   2 ,   - 2 )

π 2 :   a 2 ,   b 2 , c 2 , d 2 = ( 3 ,   + 4 ,   - 1 ,   1 )

Comparando os coeficientes visualmente não conseguimos encontrar nenhuma proporcionalidade comum. Assim, os planos são transversais.

Resposta

a )   P a r a l e l o s   C o i n c i d e n t e s

b )   P a r a l e l o s   D i s t i n t o s

c )   T r a n s v e r s a i s

Exercício Resolvido #2

Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 183-35.

Determinar a e b , de modo que os planos

π 1 : a x + b y + 4 z - 1 = 0     e     π 2 : 3 x - 5 y - 2 z + 5 = 0

sejam paralelos.

Passo 1

O problema pede para calcularmos os valores de a e b para que os planos π 1 e π 2 sejam paralelos.

Dados:

π 1 :   (   a 1 ,   b 1 , c 1 , d 1 ) = ( a ,   b ,   4 ,   - 1 )

π 2 : a 2 ,   b 2 , c 2 , d 2 = ( 3 ,   - 5 ,   - 2 ,   5 )

Passo 2

O enunciado nos pede para que os planos sejam paralelos. Não fala nada em serem paralelos distintos ou iguais. Então, pela teoria, sabemos que para serem paralelos pelo menos os 3 primeiros coeficientes devem ser proporcionais.

(   a 1 ,   b 1 , c 1 , d 1 ) = α ( a 2 ,   b 2 , c 2 , d 2 )

Substituindo as variáveis que temos:

a ,   b ,   4 ,   - 1 = α 3 ,   - 5 ,   - 2 ,   5

Igualando coordenada a coordenada, temos:

x → a = 3 α       ( 1 )

y → b = - 5 α           ( 2 )

z → 4 = - 2 α → α = - 2           ( 3 )

- 1 = α 5           ( 4 )

Substituindo α = - 2 nas expressões 1 ,   2 e 4 , obteremos:

a = - 6

b = 10

- 1 ≠ - 10

Para os planos serem paralelos a = - 6 e b = 10 , mas como - 1 ≠ - 10 sabemos que eles serão paralelos distintos.  

Resposta

a = - 6             e               b = 10

Exercício Resolvido #3

Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 183-36.

Determinar m de modo que os planos

π 1 : 2 m x + 2 y - z = 0       e     π 2 : 3 x - m y + 2 z - 1 = 0

sejam perpendiculares.

Passo 1

Temos como dados a equação geral de cada um dos planos. Mas, devemos determinar m de modo que os planos π 1 e π 2 sejam perpendiculares. Para isso, vimos na teoria que:

n 1 → ∙ n 2 → = 0

Mas, quem são n 1 → e n 2 → ? São os vetores normais aos planos. Que conseguimos retirar suas coordenadas das equações gerais dos planos.

Passo 2

Retirando os dados, temos:

n 1 → = ( 2 m ,   2 ,   - 1 )

n 2 → = ( 3 ,   - m ,   2 )

Para que os planos sejam perpendiculares devemos forçar que:

n 1 → ∙ n 2 → = 0

Substituindo os valores:

2 m ,   2 ,   - 1 ∙ 3 ,   - m ,   2 = 0

Resolvendo, temos:

6 m - 2 m - 2 = 0 → m = 1 2

Resposta

m = 1 2

Exercício Resolvido #4

Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 175.

Diga qual é a posição relativa entre planos:

π 1 : 5 x - 2 y + z + 7 = 0 ��   e     π 2 : 3 x - 3 y + z + 4 = 0

Caso eles forem transversais, determine a equação da reta formada por eles.

Passo 1

Uhh, quando começa com esse “Caso sejam transversais...” já sabemos que tem 99,99 % de chance dos planos serem transversais! Mas, como bons alunos de Geometria Analítica e Álgebra Linear, vamos provar isso!

Para os planos serem transversais, nenhum dos coeficientes pode ser proporcional. Vamos ver se isso “ser” verdade.

π 1 : 5 ,   - 2 ,   1 ,   7

π 2 : ( 3 ,   - 3 ,   1 ,   4 )

Precisamos que ( 5 ,   - 2 ,   1 ,   7 ) ≠ α ( 3 ,   - 3 ,   1 ,   4 )

Montando um sisteminha maneiro, obtemos:

5 = 3 α →   α = 5 3 - 2 = - 3 α →   α = 2 3 1 = 1 α →   α = 1 7 = 4 α →   α = 7 4

Como NENHUM dos α bate, nossos planos são de fato transversais.

Passo 2

Pô, mas além de pedir a posição relativa o moço também pediu a equação da reta formada pelos planos!

Calma, galera! É mais fácil do que parece, haha!

Pensa comigo, se dois planos são transversais, eles se cruzam (obviamente, hehe). Quando eles se cruzam forma-se uma reta comum aos dois planos! Ou seja, essa reta contém os únicos pontos em comum entre π 1 e π 2 !

Se liga nessa figura!

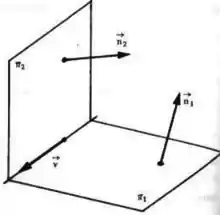
Sacou??

Então, se a gente fizer um sistema com as equações dos planos, vamos achar os pontos em comum entre eles, ou seja, os pontos da reta!

5 x - 2 y + z = - 7     I 3 x - 3 y + z = - 4     I I

De ( I ) tiramos que:

y = 5 x + z + 7 2     ( i )

De I I , temos:

z = - 4 - 3 x + 3 y     ( i i )

Substituindo i i em ( i ) :

2 y = 5 x - 4 - 3 x + 3 y + 7

y = - 2 x - 3

Logo,

z = - 4 - 3 x + 3 - 2 x - 3

z = - 9 x - 13

Com isso, nossa reta será formada pelos pontos que satisfazem as relações:

y = - 2 x - 3 z = - 9 x - 13

Para escrevermos uma equação paramétrica para a reta precisamos de um vetor diretor e de um ponto da reta. Para isso, vamos pegar dois pontos quaisquer dessa reta e calcular o vetor diretor!

r → = 1 ,   - 5 , -   22 - 0 ,   - 3 ,   - 13 = ( 1 ,   - 2 ,   - 9 )

Agora só falta um ponto! Vou usar A = ( 0 ,   - 3 ,   - 13 ) .

Logo, uma equação paramétrica de r é:

r : x = t y = - 3 - 2 t z = - 13 - 9 t

FIM 😉

Resposta

r : x = t y = - 3 - 2 t z = - 13 - 9 t

Exercício Resolvido #5

Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 185-2.

Estude a posição relativa dos planos:

π 1 : 2 x - y + z - 1 = 0

  π 2 : x - 1 2 y + 1 2 z - 9 = 0

Passo 1

O enunciado já deu para gente todos os coeficientes, então podemos comparar os planos:

π 1 :     a 1 ,   b 1 , c 1 , d 1 = ( 2 ,   - 1 ,   1 ,   - 1 )

π 2 :   a 2 ,   b 2 , c 2 , d 2 = 1 , - 1 2 , 1 2 ,   - 9

Vamos ver se:

2 ,   - 1 ,   1 ,   - 1 = α 1 ,   - 1 2 , 1 2 ,   - 9

Abrindo isso,

2 = 1 α →   α = 2 - 1 = - 1 2 α →   α = 2 1 = 1 2 α →   α = 2 - 1 = - 9 α →   α = 1 9

Como somente os três primeiros coeficientes são proporcionais,   a 1 ,   b 1 , c 1 = α a 2 ,   b 2 , c 2 , os planos são paralelos distintos!

Resposta

os planos são paralelos distintos!

Exercício Resolvido #6

Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 184-1.

Estude a posição relativa dos planos:

π 1 : X = 1 ,   0 ,   1 + λ 1 ,   1 ,   1 + µ 0 ,   1 ,   0

  π 2 : X = 0 ,   0 ,   0 + λ 1 ,   0 ,   1 + µ - 1 ,   0 ,   3

Passo 1

Já sabemos que vamos precisar passar a equação dos plano para forma geral, mas antes disso, vamos retirar os dados:

π 1 : A = ( 1 ,   0 ,   1 ) v → = ( 1 ,   1 ,   1 ) u → = ( 0 ,   1 ,   0 )           e                   π 2 : B = ( 0 ,   0 ,   0 ) r → = ( 1 ,   0 ,   1 ) s → = ( - 1 ,   0 ,   3 )

Montando e resolvendo o produto misto para achar a equação geral de cada plano temos:

Para   π 1 :

A P → ,   v → ,   u → = x - 1 y z - 1 1 1 1 0 1 0 = z - 1 - x - 1 = 0

π 1 : - x + z = 0

Para   π 2 :

B P → ,   r → ,   s → = x y z 1 0 1 - 1 0 3 = - y - 3 y = 0

π 2 :   y = 0

Agora, que temos todos os coeficientes podemos comparar os planos:

π 1 :     a 1 ,   b 1 , c 1 , d 1 = ( - 1 ,   0 ,   1 ,   0 )

π 2 :   a 2 ,   b 2 , c 2 , d 2 = ( 0 ,   1 ,   0 ,   0 )

Se   (   a 1 ,   b 1 , c 1 , d 1 ) = α ( a 2 ,   b 2 , c 2 , d 2 ) então os planos são paralelos coincidentes. Pelos coeficientes que temos:

- 1 ,   0 ,   1 ,   0 = α ( 0 ,   1 ,   0 ,   0 )

Abrindo isso,

- 1 = 0 α 0 = 1 α 1 = 0 α 0 = 0 α

Como nenhum dos coeficientes são proporcionais, os planos são transversais!

Resposta

os planos são transversais!

Exercício Resolvido #7

Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 185-2.

Calcule m para que os planos:

π 1 : X = 1 ,   1 ,   0 + λ m ,   1 ,   1 + μ ( 1 ,   1 ,   m )

  π 2 : 2 x + 3 y + 2 z + 1 = 0

Sejam paralelos distintos.

Passo 1

Primeiro precisamos passar a equação do primeiro plano para a forma geral. Do enunciado, temos:

A = 1 ,   1 ,   0

u → = m ,   1 ,   1

v → = ( 1 ,   1 ,   m )

Montando o produto misto,

A P → ,   u → ,   v → = x - 1 y - 1 z m 1 1 1 1 m

m x - m + z m + y - 1 - y m 2 - m 2 + x - 1 + z = 0

x m - 1 + y 1 - m 2 + z m - 1 + m 2 - m = 0

Vamos guardar isso aí!

Passo 2

Para os planos serem paralelos distintos,   a 1 ,   b 1 , c 1 = α a 2 ,   b 2 , c 2 . Do enunciado e do passo 1, tiramos:

π 1 :     a 1 ,   b 1 , c 1 = ( m - 1 ,   1 - m 2 ,   m - 1 )

π 2 :   a 2 ,   b 2 , c 2 = 2 ,   3 ,   2

Colocando na formulinha de paralelos distintos:

( m - 1 ,   1 - m 2 ,   m - 1 ) = α 2 ,   3 ,   2

Abrindo isso,

m - 1 = 2 α →   α = m - 1 2 1 - m 2 = 3 α →   α = 1 - m 2 3 m - 1 = 2 α →   α = m - 1 2

Como todos os “ α ' s ” precisam ser iguais, podemos igualar as equações!

m - 1 2 = 1 - m 2 3

3 m - 3 = 2 - 2 m 2

2 m 2 + 3 m - 5 = 0

Resolvendo por Báskara,

m = - 3 ± 3 2 - 4.2 . - 5 2.2

m = - 3 ± 7 4

m = 1   o u   m = - 5 2

Resposta

m = 1   o u   m = - 5 2

Exercício Resolvido #8

Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 186-3.

Mostre que os planos:

π 1 : X = 0 ,   0 ,   0 + λ - 1 , m ,   1 + μ ( 2 ,   0 ,   1 )

  π 2 : X = 1 ,   2 ,   3 + α m ,   1 ,   0 + β ( 1 ,   0 ,   m )

São transversais, para todo m ∈ R .

Passo 1

Primeiro precisamos passar a equação dos planos para a forma geral. Do enunciado, temos:

Para π 1 :

A = 0 ,   0 ,   0

u → = - 1 ,   m ,   1

v → = ( 2 ,   0 ,   1 )

Montando o produto misto,

A P → ,   u → ,   v → = x y z - 1 m 1 2 0 1

m x + 2 y - ( - y + 2 m z ) = 0

m x + 3 y - 2 m z = 0

Para π 2 :

B = 1 ,   2 ,   3

r → =   m ,   1 ,   0

s → = ( 1 ,   0 ,   m )

Montando o produto misto,

B P → ,   r → ,   s → = x - 1 y - 2 z - 3 m 1 0 1 0 m

m x - m - ( m 2 y - 2 m 2 + z - 3 ) = 0

m x - m 2 y - z + ( 2 m 2 - m + 3 ) = 0

Passo 2

Para os planos serem transversais,   a 1 ,   b 1 , c 1 , d 1 ≠ α a 2 ,   b 2 , c 2 , d 2 . Do passo 1, tiramos:

π 1 :     a 1 ,   b 1 , c 1 , d 1 = ( m ,   3 ,   - 2 m ,   0 )

π 2 :   a 2 ,   b 2 , c 2 , d 2 = m ,   - m 2 ,   - 1 ,   2 m 2 - m + 3

Colocando na formulinha:

( m ,   3 ,   - 2 m ,   0 ) ≠ α m ,   - m 2 ,   - 1 ,   2 m 2 - m + 3

Abrindo isso,

m = m α →   α = 1   ( i ) 3 = - m 2 α →   α = 3 - m 2   ( i i ) - 2 m = - 1 α →   α = 2 m   ( i i i ) 0 = α 2 m 2 - m + 3 → α = 0   ( i v )

Agora precisamos provar todos esses “ α ' s ” serão diferentes (pois os planos precisam ser transversais), independente do valor de m !

De cara já vemos que os “ α ' s ” de ( i ) e ( i v ) serão diferentes, logos os planos nunca serão paralelos coincidentes.

Para os planos não serem paralelos distintos (para só sobrar a opção transversais), precisamos mostrar que os “ α ' s ” ( i i ) e ( i i i ) nunca serão iguais a 1 (que é o valor de α de ( i ) ).

Vamos tentar colocar α = 1 em ( i i ) e ( i i i ) :

1 = 3 - m 2 → m 2 = - 3 1 = 2 m → m = 1 2

Na primeira equação temos um número ao quadrado igual a um número negativo! Sabemos que isso terá um número complexo como resposta e, como estamos focando nos números reais, essa resposta não é válida! Logo   a 1 ,   b 1 , c 1 , d 1 ≠ α a 2 ,   b 2 , c 2 , d 2 irá ocorrer independente do valor de m e os planos serão sempre transversais!

Resposta

os planos serão sempre transversais!

Exercícios de Livros Relacionados

Obtenha um vetor normal ao plano π em cada caso:a) π contém A = ( 1 ,1 ,1 ) , B = ( 1 ,0 ,1 ) e C = ( 1 ,2 ,3 ) .b) π : x - 2 y + 4 z + 1 = 0 .c) π : X = 1 ,2 ,0 + λ1 ,- 1 ,1 + μ( 0 ,1 ,- 2 ) .
As equações X = 0,0 , 0 + t α 1,2 , 4 e X = 1,0 , - 2 + t - 1 , - 1 , - 1 , t ∈R , descrevem os movimentos de duas partículas. Determine o valor de α para que haja colisão. Em que instante ela ocorre?
Decomponha o vetor u → = ( - 3 ,4 ,- 5 ) em duas parcelas, uma paralela e outra ortogonal ao plano de equação vetorial X = 1 ,- 2 ,0 + λ- 1 ,0 ,1 + μ( 0 ,0 ,- 1 ) .
O vetor ( 1 ,1 ,m ) é normal ao plano π , que contém a intersecção dos planos π 1 : x - y + z + 1 = 0 e O y z . Determine m e obtenha uma equação geral de π .
Representar graficamente os planos de equações:3 x + 4 y + 2 z - 12 = 0