Distância entre ponto e reta
Produzido por Aline BuzziTeoria
E aí, você chegou no Responde Aí! E nossa missão é te ajudar a se dar bem na prova! Então vamos lá falar sobre distância entre ponto e reta
Relembrando a distância entre dois pontos
Pra entender direitinho como calcular a distância entre ponto e reta, primeiro você precisa lembrar que para calcular a distância entre dois pontos
Distância entre ponto e reta
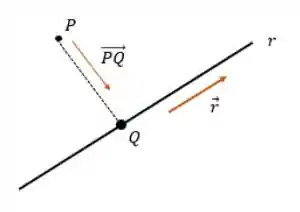
Já parou para pensar que entre um ponto e uma reta existem várias distâncias? Como assim???
Olha só:
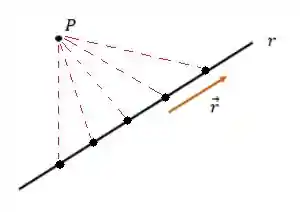
O que interessa de verdade pra gente é a menor distância entre ponto e reta. Essa menor distância acontece quando houver um ângulo de
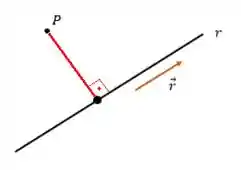
Então, para calcular a distância entre o ponto e uma reta primeiro temos que achar um ponto Q que faça um ângulo de
Como calcular a distância entre ponto e reta?
Para calcular a distância entre dois pontos a gente segue os seguintes passo:
Para calcular a distância do ponto
- Usar a equação da reta para encontrar um ponto
em função de - Calculamos o vetor
- Por definição
faz com . Então usamos para encontrar . - Aplicamos o valor de
no ponto - Calcular a distância entre
e com a fórmula da distância entre pontos
Exemplo
Calcule a distância entre o ponto
Passo 1: Primeiro precisamos encontrar um ponto que forme
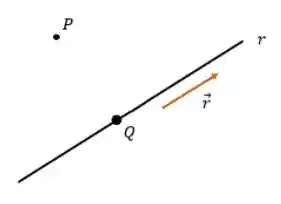
Nós sabemos que
Passo 2: Pronto, agora podemos encontrar o vetor
Passo 3: Beleza. É agora que vem o pulo do gato! A gente sabe que o vetor
Logo:
Passo 4: Agora, é só aplicar o valor de
Passo 5: E pra finalizar, é só a gente usar a fórmula da distância entre dois pontos:
Prontinho!! Calculamos a distância entre o ponto
Que tal agora dar uma olhada numa super vídeo aula sobre o tema?!
Agora dá uma olhada aqui em baixo pra ver um monte de exercícios! 👇