Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Distância entre Duas Retas

Produzido por Matheus dos Santos Soares
Ver Todos os Exercícios

Teoria

Como calcular a distância entre duas retas?

Topa descobrir agora? Então bora lá!

Vamos separar em três casos: retas concorrentes, retas paralelas e retas reversas.

RETAS CONCORRENTES

Esse caso é o mais simples e não tem nenhum mistério. Retas concorrentes se cruzam, então a distância entre elas é ZERO!

RETAS PARALELAS

Para esse caso, temos um passo a passo a ser seguido:

Passo a passo para calcular distância entre duas retas paralelas
Passo a passo para calcular distância entre duas retas paralelas

Eu sei que esse passo a passo assim é bem complicado de entender, então vamos aplicá-lo em um exemplo.

Imagine as retas e

Primeiro escolhemos um ponto de uma das retas. Podemos escolher o ponto que pertence a reta .

Agora precisamento considerar um ponto qualquer que pertence a reta :

Agora, temos que calcular o vetor ortogonal ao vetor diretor de uma das retas (nesse caso, pode ser o vetor diretor de qualquer uma das retas, pois como elas são paralelas os seus vetores diretores são poporcionais).

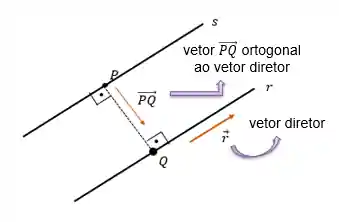
Vetor PQ otogonal ao vetor diretor
Vetor PQ otogonal ao vetor diretor

Calculando esse vetor:

Sabendo que o vetor é ortogonal à (vetor diretor) o produto escalar entre eles tem que ser zero. Então, se considerarmos , temos:

Sabendo conseguimos achar com clareza o vetor :

E agora, para acharmos a distância temos que fazer o módulo desse vetor:

E ACABOU!! Demorou mais foi hahaha

Mas ainda não acabou o conteúdo todo, falta só mais um caso...

Não desiste agora

RETAS REVERSAS

Esse caso aqui é bem parecido com as retas paralelas, você vai tirar de letra!

Primeiro vamos escrever os dois pontos e genericamente, sendo pertencente à reta e pertencente à reta .

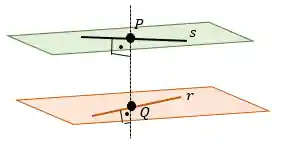
Depois de escrito os pontos vamos escrever um vetor que seta ortogonal ao vetor diretor de cada uma das retas. Ou seja, faremos:

Vetor
Vetor

Quando resolvermos essas duas equações acharemos um valor para e outro ara , podendo assim encontrar os ponto e . Por fim, é só calcular a distância.

Pegou a dinâmica?

Vamos praticar agora com muito exercícios?

Ahhh... quase ia me esquecendo... Você pode conferir esse conteúdo em vídeo também 😱

Dá uma olhada aqui 👇🏽

Exercícios Resolvidos

Exercício Resolvido #1

Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 193-3.

Calcular a distância entre as retas r : y = - 2 x + 3 z = 2 x e s : x = - 1 - 2 t y = 1 + 4 t z = - 3 - 4 t

Passo 1

Simbora começar!

A primeira coisa que precisamos saber é se as nossas retas são paralelas distintas ou reversas.

Lembra lá da definção de retas paralelas??

Duas retas são paralelas se seus vetores diretores obedecem a relação

r → = α s →

Vamos ver se isso é verdade!

Considerando   r → = ( 1 ,   - 2 ,   2 ) e   s → = ( - 2 ,   4 ,   - 4 ) , temos:

1 ,   - 2 ,   2 = α ( - 2 ,   4 ,   - 4 )

α = - 1 2

Logo, as retas são paralelas!!

Passo 2

Agora que já sabemos que a retas são parelelas, o exercício fica igual a distância entre ponto e reta!

Vamos escolher um ponto P da reta r :

Se x = 0 ,   P = 0 ,   3 ,   0

E um ponto genérico Q da reta s é:

Q = ( - 1 - 2 t ,   1 + 4 t ,   - 3 - 4 t )

Agora calculamos   P Q →

P Q → = Q - P = - 1 - 2 t ,   1 + 4 t ,   - 3 - 4 t - 0 ,   3 ,   0 = ( - 1 - 2 t ,   - 2 + 4 t ,   - 3 - 4 t )

Passo 3

Da equação da reta s tiramos que s → = ( - 2 ,   4 ,   - 4 ) e já descobrimos que

  P Q → = - 1 - 2 t ,   - 2 + 4 t ,   - 3 - 4 t

Também sabemos da teoria que o vetor diretor da reta r e o vetor P Q → são ortogonais, logo:

P Q → ∙ s → = 0

Calculando:

- 1 - 2 t ,   - 2 + 4 t ,   - 3 - 4 t ∙ - 2 ,   4 ,   - 4 = 2 + 4 t - 8 + 16 t + 12 + 16 t = 0 → t = - 1 6

Agora que achamos que t = - 1 6 podemos calcular Q :

Q = - 1 - 2 t ,   1 + 4 t ,   - 3 - 4 t → Q = - 2 3 , 1 3 ,   - 7 3

Passo 4

Agora, para terminar (UFA!) vamos achar a distancia entre o ponto P e a reta s , é só calcular a distância entre os ponto P ( 0 ,   3,0 ) e Q = - 2 3 , 1 3 , - 7 3 .

Não lembra a fórmula??

A gente relembra!

d P , Q = x - x 0 2 + ( y - y 0 ) 2 + ( z - z 0 ) 2

Substituindo os valores:

d P , Q = 0 + 2 3 2 + 3 - 1 3 2 + 0 + 7 3 2 = 13 u . c

Resposta

d P , Q = 13 u . c

Exercício Resolvido #2

Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 202-5c.

Calcular a distância entre as retas r : x = 3 y = 2 e s : x = 1 y = 4

Passo 1

Eita, tá estranho essas retas ai, como é isso??

Galera, reparem que o que temos são pontos! Então é só calcular a distância entre eles!

Passo 2

Os pontos são P r = 3 ,   2 e P S = 1,4 .

A fórmula para distância entre pontos é:

d P , Q = x - x 0 2 + y - y 0 2 + ( z - z 0 ) 2

Como não temos coordenada z , nossa fórmula fica:

d P r , P s = 3 - 1 2 + ( 2 - 4 ) 2

d P r , P s = 8 = 2 2

Resposta

d P r , P s = 8 = 2 2   u . c

Exercício Resolvido #3

Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 195-4.

Calcular a distância entre as retas r : y = 1 x + 2 = z - 4 - 2 e s : x = 3 y = 2 t - 1 z = - t + 3

Passo 1

Primeiramente precisamos saber se as nossas retas são paralelas distintas ou reversas.

Já sabemos que duas retas são paralelas se seus vetores diretores obedecem a relação

r → = α s →

Vamos ver se isso é verdade!

Considerando   r → = ( 1 ,   0 ,   - 2 ) e   s → = ( 0 ,   2 ,   - 1 ) , temos:

1 ,   0 , -   2 = α ( 0 ,   2 ,   - 1 )

Abrindo isso, temos:

1 = 0 α 0 = 2 α - 2 = - 1 α

Olhando para primeira equação já vemos um problema, pois obtemos uma indeterminação α = 1 0 . Com isso nossas retas não são paralelas.

Logo, as retas são reversas!!

Passo 2

Bem, agora precisamos pegar um ponto de cada reta!!

Vou passar a equação da reta r para paramétrica para ficar mais fácil de visualizar

r : x + 2 = h y = 1 z - 4 - 2 = h

r : x = h - 2 y = 1 z = - 2 h + 4

Com isso, um ponto P da reta r é:

P = ( - 2 ,   1 ,   4 )

Para a reta s , um ponto Q é:

Q = ( 3 ,   - 1 ,   3 )

Com isso, conseguimos calcular o vetor   P Q →

P Q → = 3 ,   - 1 ,   3 - - 2 ,   1 ,   4

P Q → = ( 5 ,   - 2 ,   - 1 )

Passo 3

Agora que já possuímos os três vetores que geram o paralelepípedo, vamos relembrar a fórmula:

D r ,   s = r → ,   s → ,   P Q → r → × s →

Calculando os termos,

r → ,   s → ,   P Q → = 1 0 - 2 0 2 - 1 5 - 2 - 1 = 16

r → × s → = i → j → k → 1 0 - 2 0 2 - 1 = 4 ,   1 ,   2

r → × s → = ( 4 ,   1 ,   2 ) = 21

Logo,

D r ,   s = 16 21 u . c

UHULESSSS 😊

Resposta

D r ,   s = 16 21 u . c

Exercício Resolvido #4

Elaboração própria

Calcular a distância entre as retas r : x = 2 + 2 t y = 3 + 4 t z = 5 + t e s : x = 2 + 2 h y = - 1 + 2 h z = - 3 + h

Passo 1

Vamos ver se as nossas retas são paralelas distintas ou reversas.

Já sabemos que duas retas são paralelas se seus vetores diretores obedecem a relação

r → = α s →

Vamos ver se isso é verdade!

Considerando   r → = ( 2 ,   4 ,   1 ) e   s → = ( 2 ,   2 ,   1 ) , temos:

2 ,   4,1 = α ( 2 ,   2 ,   1 )

Abrindo isso, temos:

2 = 2 α →   α = 1 4 = 2 α →   α = 2 1 = 1 α →   α = 1

Como os valores de α não são todos iguais as retas são reversas!!

Passo 2

Vamos resolver esse exercício usando a primeira opção de resolução para você ver que dá certo também!

Primeiro, escrevemos um ponto genérico para cada reta:

Para reta r → P = 2 + 2 t ,   3 + 4 t ,   5 + t

Para reta s → Q = ( 2 + 2 h ,   - 1 + 2 h ,   - 3 + h )

Bem, agora podemos calcular o vetor   P Q →

P Q → = 2 + 2 h ,   - 1 + 2 h ,   - 3 + h - 2 + 2 t ,   3 + 4 t ,   5 + t

P Q → = ( 2 h - 2 t ,   - 4 + 2 h - 4 t ,   - 8 + h - t )

Passo 3

Vamos fazer os produtos internos!

P Q → ∙ r → = 0 e   P Q → ∙ s → = 0

P Q → ∙ r → = 2 h - 2 t ,   - 4 + 2 h - 4 t ,   - 8 + h - t ∙ 2 ,   4 ,   1 = 0

P Q → ∙ r → = 13 h - 21 t - 24 = 0

P Q → ∙ s → = 2 h - 2 t ,   - 4 + 2 h - 4 t ,   - 8 + h - t ∙ 2 ,   2 ,   1 = 0

P Q → ∙ s → = 9 h - 13 t - 16 = 0

Montando um sisteminha para achar t e h :

13 h - 21 t = 24     ( I ) 9 h - 13 t = 16     ( I I )

De ( I I ) tiramos que h = 16 + 13 t 9 . Substituindo em ( I ) :

13 16 + 13 t 9 - 21 t = 24

Igualando os denominadores

208 + 169 t - 189 t = 216

t = - 2 5

Logo, h = 16 + 13 t 9 = 6 5 .

Com isso podemos achar P e Q !

P = 2 + 2 t ,   3 + 4 t ,   5 + t = 6 5 , 7 5 , 23 5

Q = 2 + 2 h ,   - 1 + 2 h ,   - 3 + h = 22 5 , 7 5 ,   - 9 5

Passo 4

Por fim, calculamos d ( P , Q )

d P , Q = x - x 0 2 + y - y 0 2 + z - z 0 2

Substituindo os valores:

d P , Q = 6 5 - 22 5 2 + 7 5 - 7 5 2 + 23 5 - - 9 5 2 = 16 5 u . c

Resposta

16 5 u . c

Exercício Resolvido #5

Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 201-5a.

Calcular a distância entre as retas r : x = 0 y = z e s : y = 3 z = 2 x

Passo 1

Vamos ver se as nossas retas são paralelas distintas ou reversas.

Já sabemos que duas retas são paralelas se seus vetores diretores obedecem a relação

r → = α s →

Para achar um vetor diretor para r , podemos escolher dois pontos quaisquer de r e subtraí-los

r → = 0,2 , 2 - 0,1 , 1 = ( 0,1 , 1 )

Fazendo o mesmo para s , obtemos

s → = ( 1,0 , 2 )

Agora vamos checar se as retas são paralelas ou não:

0,1 ,   1 = α ( 1 ,   0 ,   2 )

Abrindo isso, temos:

0 = 1 α →   α = 0 1 = 0 α → α = 1 0 1 = 2 α →   α = 1 2

Olhando para segunda equação já vemos um problema, pois obtemos uma indeterminação α = 1 0 , além disso nenhum valor de α bate!

Logo, as retas são reversas!!

Passo 2

Bem, agora precisamos pegar um ponto de cada reta!!

Um ponto P da reta r é:

P = ( 0,3 ,   3 )

Para a reta s , um ponto Q é:

Q = ( 3,3 ,   6 )

Com isso, conseguimos calcular o vetor   P Q →

P Q → = 3 ,   3 ,   6 - 0 ,   3 ,   3

P Q → = ( 3 ,   0   3 )

Passo 3

Agora já possuímos os três vetores que geram o paralelepípedo!

Relembrando a fórmula:

D r ,   s = r → ,   s → ,   P Q → r → × s →

Calculando os termos,

r → ,   s → ,   P Q → = 0 1 1 1 0 2 3 0 3 = 3

r → × s → = i → j → k → 0 1 1 1 0 2 = 2 ,   1 ,   - 1

r → × s → = ( 2 ,   1 ,   - 1 ) = 6

Logo,

D r ,   s = 3 6 u . c

UHULESSSS 😊

Resposta

D r ,   s = 3 6 u . c

Exercício Resolvido #6

Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 202-5b.

Calcular a distância entre as retas r que passa pelos pontos A ( 1,0 , 1 ) e B = ( - 1 ,   - 1,0 ) e s que passa pelos pontos C ( 0 ,   1 ,   - 2 ) e D 1 ,   1 ,   1 .

Passo 1

Bem, com essas informações conseguimos achar os vetores diretores de cada reta!

Para reta r :

r → = - 1 ,   - 1 ,   0 - 1 ,   0 ,   1 = ( - 2 ,   - 1 ,   - 1 )

Para reta s :

s → = 1,1 , 1 - 0 ,   1 ,   - 2 = ( 1 ,   0 ,   3 )

Com isso, vamos ver se as retas são paralelas distintas ou reversas.

Já sabemos que duas retas são paralelas se seus vetores diretores obedecem a relação

r → = α s →

Substituindo os valores,

( - 2 ,   - 1 ,   - 1 ) = α ( 1 ,   0 ,   3 )

Abrindo isso, temos:

- 2 = 1 α - 1 = 0 α - 1 = 3 α

Mais uma vez obtemos uma indeterminação α = - 1 0 na segunda equação. Com isso nossas retas não são paralelas.

Logo, as retas são reversas!!

Passo 2

Agora precisamos pegar um ponto de cada reta! Isso o enunciado já nos deu!

Com isso, um ponto P da reta r é:

P = ( 1 ,   0 ,   1 )

Para a reta s , um ponto Q é:

Q = ( 0 ,   1 ,   - 2 )

Agora basta calcular o vetor   P Q →

P Q → = 0 ,   1 ,   - 2 - 1 ,   0 ,   1

P Q → = ( - 1 ,   1 ,   - 3 )

Passo 3

Agora que já possuímos os três vetores que geram o paralelepípedo, vamos relembrar a fórmula:

D r ,   s = r → ,   s → ,   P Q → r → × s →

Calculando os termos,

r → ,   s → ,   P Q → = - 2 - 1 - 1 1 0 3 - 1 1 - 3 = 5

r → × s → = i → j → k → - 2 - 1 - 1 1 0 3 = - 3 ,   5 ,   1

r → × s → = ( - 3 ,   5 ,   1 ) = 35

Logo,

D r ,   s = 5 35 u . c

UHULESSSS 😊

Resposta

D r ,   s = 5 35 u . c

Exercício Resolvido #7

Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 202-5d.

Calcular a distância entre as retas r : x = 1 - t y = 2 + 3 t z = - t e o eixo dos x .

Passo 1

Bem, um vetor diretor para o eixo x pode ser   x → = 1,0 , 0

O vetor diretor de r é   r → = - 1 ,   3 ,   - 1

De cara vemos que essas retas não são paralelas, pois  x → não é múltiplo de   r → .

Com isso, as retas são reversas!

Passo 2

Agora precisamos pegar um ponto de cada reta!!

Um ponto P da reta r é:

P = ( 1 ,   2 ,   0 )

Para o eixo x , um ponto Q é:

Q = ( 2 ,   0 ,   0 )

Com isso, conseguimos calcular o vetor   P Q →

P Q → = 2 ,   0 ,   0 - 1 ,   2 ,   0

P Q → = ( 1 ,   - 2 ,   0 )

Passo 3

Agora que já possuímos os três vetores que geram o paralelepípedo, vamos relembrar a fórmula:

D r ,   s = r → ,   s → ,   P Q → r → × s →

Calculando os termos,

r → ,   s → ,   P Q → = - 1 3 - 1 1 0 0 1 - 2 0 = - 2 = 2

r → × s → = i → j → k → - 1 3 - 1 1 0 0 = 0 , -   1 , - 3

r → × s → = ( 0 ,   - 1 ,   - 3 ) = 10

Logo,

D r ,   s = 2 10 u . c

Acabou!!!!

Resposta

D r ,   s = 2 10 u . c

Exercício Resolvido #8

Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 202-5e.

Calcular a distância entre as retas r : x = y = z - 2 e s : y = x + 1 z = x - 3

Passo 1

Primeiro vamos organizar essas retas!

Da reta r conseguimos ver que  r → = ( 1 ,   1,1 ), já que esses são os denominadores da minha equação (se você não lembra muito bem disso, dá uma olhada em “Introdução à Reta”, nas equações simétricas 😊).

Vamos passar a equação da reta s para forma simétrica para ficar mais fácil visualizar:

Da primeira equação (a de y ), tiramos que:

x = y - 1

Da segunda equação (a de z ), temos:

x = z + 3

Igualando obtemos:

x = y - 1 = z + 3

Com isso obtemos o vetor diretor   s → = 1 ,   1 ,   1 .

Como   r → = s → , nossas retas são paralelas!

Passo 2

O exercício de retas paralelas está tão lá atrás que você nem deve lembrar mais como faz!

Zero problemas, a gente relembra junto!

Primeiro a gente escolhe um ponto P de uma das retas. Vou escolher o ponto P = 1 ,   1 ,   3 da

reta r .

Depois escrevemos o ponto Q da reta s genericamente. Para isso, faremos:

s : x = y - 1 = z + 3 = t

x = t

y = t + 1

z = t - 3

Logo, Q = ( t ,   t + 1 ,   t - 3 )

Com isso, conseguimos calcular o vetor   P Q →

P Q → = t ,   t + 1 , t - 3 - 1 ,   1 ,   3

P Q → = ( t - 1 ,   t ,   t - 6 )

Passo 3

Lá na teoria vimos que   P Q → é ortogonal aos vetores diretores das nossas “retosas”. Então o produto interno entre eles precisa dar zero!! Vou escolher fazer o produto interno com s → , mas com r → também funciona!

P Q → ∙ s → = t - 1 ,   t ,   t - 6 ∙ 1 ,   1,1 = 0

t - 1 + t + t - 6 = 0

t = 7 3

Assim, conseguimos achar o ponto Q

Q = t ,   t + 1 ,   t - 3 = 7 3 , 10 3 ,   - 2 3

Passo 4

Por fim, é só calcular d ( P , Q ) !

d P , Q = x - x 0 2 + y - y 0 2 + z - z 0 2

d P , Q = 7 3 - 1 2 + 10 3 - 1 2 + - 2 3 - 3 2 = 186 3 u . c

E FIMMMMM 😊

Resposta

D r ,   s = 186 3 u . c

Exercício Resolvido #9

Jacir J. Venturi, Álgebra vetorial e Geometria analítica, 10ª ed., Curitiba, 2015, Pp 220 -1a.

Sendo r 1 : x + z - 2 = 0 y - 1 = 0 e r 2 : x - 2 y - 1 = 0 z - 1 = 0 . Calcular a distância entre elas.

Passo 1

Primeiro vamos organizar essas retas.

Começando com r 1 , temos que dois pontos são P 1 = ( 1 ,   1 ,   1 ) e P 2 = ( 2 ,   1 ,   0 ) .

Com isso,   r 1 → = P 1 P 2 → = ( 1 ,   0 ,   - 1 ) .

Assim,

r 1 : x ,   y ,   z = 1 ,   1 ,   1 + 1 ,   0 ,   - 1 t

Agora para r 2 ! Dois pontos são Q 1 = ( 1 ,   0 ,   1 ) e Q 2 = ( 3 ,   1 ,   1 ) e,

r 2 → = Q 1 Q 2 → = ( 2 ,   1 ,   0 )

Com isso,

r 2 : x ,   y ,   z = 1 ,   0 ,   1 + 2 ,   1 ,   0 h

Passo 2

Agora, vamos ver se as retas são paralelas. Para isso, temos que ver se

r 1 → = α r 2 →

1 ,   0 ,   - 1 = α 2 ,   1 ,   0

Abrindo isso,

1 = 2 α →   α = 1 2 0 = 1 α →   α = 0 - 1 = 0 α → α = - 1 0 = i n d e t e r m i n a ç a o

Como nenhum dos valores de α bate, as retas são reversas!!

Passo 3

Bem, agora precisamos pegar um ponto de cada reta!!

Do passo 1 temos

P r 1 = ( 1 ,   1 ,   1 ) e P r 2 = ( 1 ,   0 ,   1 )

Com isso, conseguimos calcular o vetor   P r 1 P r 2 →

P r 1 P r 2 → = 1 ,   0 ,   1 - 1 ,   1 ,   1

P r 1 P r 2 → = ( 0 ,   - 1 ,   0 )

Passo 4

Agora que já possuímos os três vetores que geram o paralelepípedo, vamos relembrar a fórmula:

D r ,   s = r → ,   s → ,   P Q → r → × s →

Calculando os termos,

r 1 → ,   r 2 → ,   P r 1 P r 2 → = 1 0 - 1 2 1 0 0 - 1 0 = 2

r 1 → × r 2 → = i → j → k → 1 0 - 1 2 1 0 = 1 ,   - 2 ,   1

r 1 → × r 2 → = ( 1 ,   - 2 ,   1 ) = 6

Logo,

D r 1 ,   r 2 = 2 6 u . c

Multiplicando por 6 6   ,

D r 1 ,   r 2 = 6 3 u . c

UHULESSSS 😊

Resposta

D r 1 ,   r 2 = 2 6 u . c = 6 3 u . c

Exercícios de Livros Relacionados

Repita o exercício resolvido anterior com os mesmos sistemas de coordenadas, substituindo a equação vetorial pora) X = 0 ,0 ,0 + λ ( 0 ,0 ,1 ) b) X = 1 2 ,2 ,0 + λ ( 1 ,4 ,- 2 )
Qual é a distância da origem à reta 5 x - 2 y = 8 ?
Obtenha uma equação vetorial da reta r que contém A = ( 0 ,0 ,3 ) , está contida em π : x + z = 3 e dista 3 de O y .
Determine a reta r que contém o ponto A , é paralela ao plano π e dista d da reta s .(b) A = 1 ,2 ,0π : x + y + z = 1s : X = 0 ,3 ,2 + λ ( 1 ,1 ,0 ) d = 2
Calcule a distância do segmento A B à reta s , nos casos(a) A = 2 ,3 ,0B = - 1 ,0 ,6s : X = 0 , - 3 ,- 1 + λ ( 1 ,- 1 ,0 )