Distância entre Reta e Plano
Produzido por Aline BuzziTeoria
Introdução
Beleza, antes de começarmos a calcular distâncias, vamos relembrar as possíveis posições relativas entre uma reta e um plano:
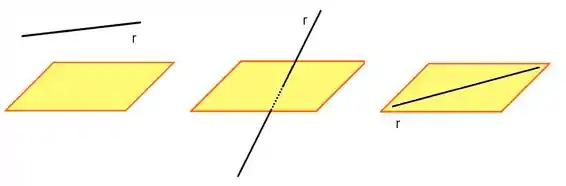
Aí eu te pergunto: Quando faz sentido calcular a distância entre uma reta e um plano?
Vamos analisar as distâncias em cada caso:
Se uma reta for transversal a um plano , então a distância entre a reta e o plano é ZERO (já que a reta vai literalmente cruzar o plano).
A mesma coisa acontecerá quando a reta está contida no plano, a distância será ZERO.
Já se a reta for paralela ao plano, teremos uma distância para ser calculada! Então só vamos calcular a distância entre retas e planos quando esses forem paralelos distintos entre si.
Encontrando a distância entre Reta e Plano
Se pararmos para pensar existem várias distâncias possíveis entre um plano e uma reta:
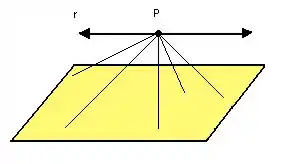
A distância que queremos será a menor possível, ou seja, a distância perpendicular:
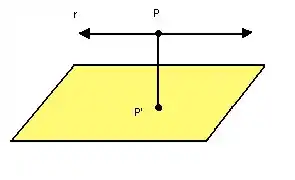
Nosso objetivo é calcular essa distância! Analisando essa situação, percebemos que se trata na verdade da distância entre um ponto e o plano, concorda?! Vamos aprender a calcular essa distância.
Calculando a distância entre Reta e Plano
Então vamos calcular essa distância e faremos da seguinte maneira:
- Escolheremos um ponto qualquer pertencente à reta;
- Calcularemos a distância do ponto escolhido até o plano utilizando a fórmula da distância entre ponto e plano apresentada anteriormente.
Vamos fazer um exemplo?!
Qual é a distância entre o plano e a reta abaixo?
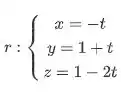
Para calcular a distância, primeiro escolhemos um ponto qualquer da reta. Fazendo , eu vou escolher o ponto .
Agora é só usar a fórmula de distância entre ponto e plano!
Não lembra?? Zero problemas, a gente relembra!
Vamos colocar nossos valores na fórmula:
Logo,
E essa é exatamente a distância entre a reta e o plano !!
Show de bolinhas!!! Acabamos essa teoria!!!
Se liga nos exercícios para ficar tudo chuchu no mel!!
Encontrando a distância entre Reta e Plano
Calculando a distância entre Reta e Plano
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Calcule a distância entre a reta e o plano .
Passo 1
Queremos achar a distância entre uma reta e um plano! Como vimos na teoria é só pegar um ponto pertencente à reta e calcular a distância entre ponto e plano que já conhecemos. Na verdade estamos esquecendo de um passo primordial!! Você sabe qual é?

Lembra que lá na teoria falamos que a reta e o plano podem ser paralelos, então, podemos calcular a distância entre eles, mas se a reta e o plano forem transversais por definição a distância é ZERO?!
Passo 2
Assim, vamos primeiro checar qual a posição relativa entre o plano e a reta! Pela teoria sabemos que se e , então se:
O plano e a reta são transversais. Se temos que e , então
Portanto, a reta e o plano são transversais. Assim, a distância entre eles é ZERO.
Viu!! Um detalhe pode poupar tempo!! Então, nunca esqueça de fazer essa verificação se o enunciado não falar nada sobre a posição relativa entre a reta e o plano.
Resposta
Exercício Resolvido #2
Elaboração própria
Ache a distância entre a reta e o plano , sabendo que a reta é a paralela ao plano.
Passo 1
Como o enunciado diz que a reta é paralela ao plano, podemos partir direto para o ataque! Se não fosse falado nada no enunciado, recomendo fortemente que você verifique se a reta e o plano são transversais ou não, porque isso pode te economizar tempo.
Passo 2
Partindo para o ataque, sabemos que e . Sabemos também a formulinha:
Logo,
Resposta
Exercício Resolvido #3
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 203-12.
Determinar a distância da reta
- Ao plano
- Ao plano
Passo 1
Temos duas maneiras de resolver esse exercício, vamos resolver a letra “a” da forma mais tradicional (e mais longa) e a letra ”b” de uma forma mais rápida.
Mas vamos começar pela “a”
Lembrando lá da nossa “formulosa” (essa aqui de baixo), precisamos de um ponto da reta e da equação geral do plano.
Um ponto da reta pode ser , mas quem é o meu plano??
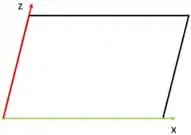
Ahhh, maneiro. Mas qual é a equação dele mesmo??
Vamos descobrir, haha.
Olhando para reta do eixo , tiramos que um vetor diretor é , fazendo o mesmo para o eixo , temos Se a gente fizer vamos achar o vetor normal ao nosso plano !
Achamos , agora vamos substituir na forma geral da equação do plano:
Para descobrir , basta substituir um ponto do plano na equação acima. Um ponto de é , logo
Com isso, a equação geral do plano é
Passo 2
Agora que sabemos , e , podemos substituir na fórmula!
Passo 3
Vamos resolver a letra “b” rapidinho!
O ponto da reta pode ser o mesmo, logo .
Agora, pensa comigo. O plano é o plano formado pelos eixos e , deixando o eixo excluidão. Então, o plano é exatamente o plano .
Com isso, , .
É só colocar na fórmula e partir para o abraço!
E zefini!
Resposta
Exercício Resolvido #4
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 234-19.
Ache os pontos da reta que equidistam dos planos
Passo 1
Esse exercício é parecido com o anterior!! Mas, agora, queremos descobrir os pontos da reta que são equidistantes dos planos e . Para isso, se temos um ponto que pertence à reta , então:
Passo 2
Precisamos primeiro achar o ponto genérico ! Para isso, vamos primeiro colocar a equação que nos foi dada na forma simétrica para então podermos tirar os dados e escrever a equação vetorial da reta:
Então, e . Montando a equação vetorial temos:
Assim, conseguimos escrever :
Passo 3
Sabendo e sabendo que para e . Podemos colocar os valores na fórmula:
Igualando :
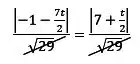
Elevando os dois membros ao quadrado:
Passo 4
Agora que sabemos que , podemos substituir em :
Então, os pontos equidistantes são: