A força de arrasto sobre uma esfera lisa, estacionária, depende de , , e . Obter um conjunto de grupos adimensionais que possam ser usados para correlacionar dados experimentais.
Passo 1
Partiu fazer a análise dimensional para encontrar o conjunto de grupos adimensionais que o exercícios pediu!
Começando com a separação sas variáveis e suas dimensões:
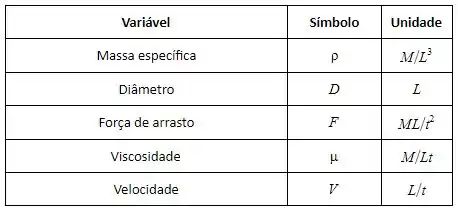
Temos cinco variáveis e três dimensões primárias , então:
Vamos ter dois grupos adimensionais!
Passo 2
Como temos três dimensões primárias, vamos ter três parâmetros repetidos! Vamos escolher, como parâmetro repetido, a massa específica, o diâmetro e a velocidade, ok? Nossos grupos adimensionais, serão:
Agora vamos escrever cada um deles em relação às dimensões. Lembrando que nossos coeficientes precisam ser iguais a zero, temos:
Isso nos diz que:
Então temos:
e
Sendo assim teremos:
Portanto nosso primeiro grupo adimensional será:
Passo 3
Agora vamos fazer o mesmo para o segundo grupo adimensional!
Isso nos diz que:
Então temos:
e
Sendo assim:
Portanto nosso segundo grupo adimensional será:
Podemos então tirar a relação funcional, dos dois grupos adimensionais, sendo ela:
Show de bolinhas!
Resposta
Os grupos adimensionais são:
A relação funcional é: