Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Análise Dimensional

Ver Teoria
Exercício 51234678

Enunciado

Num processo de galvanização, a velocidade com que os íons se movem em soluções eletrolíticas diluídas para eletrodo em forma de disco, é função da velocidade de difusão de massa dos íons. O processo depende do controle das variáveis abaixo. Obtenha os grupos adimensionais para estas variáveis, onde K , μ e D estão cada um em grupos diferentes.

Dados:

K = coeficiente de transferência de massa m / s

d = diâmetro do disco m

ρ = massa específica k g / m 3

D = coeficiente de difusão m 2 / s

a = velocidade angular 1 / s

μ = viscosidade k g / m . s

Passo 1

Vamos fazer essa análise dimensional!

Começando com a separação sas variáveis e suas dimensões, ok?

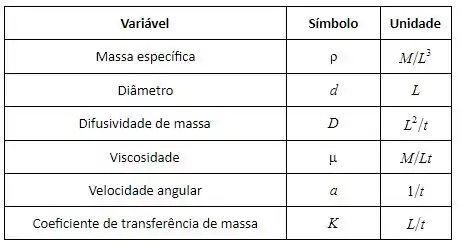
Temos seis variáveis e três dimensões primárias , então:

i = 6 - 3

i = 3

Vamos ter três grupos adimensionais!

Passo 2

O enunciado já disse pra gente que as grandezas que não se repetem são: K , μ e D … Então elas ficaram cada uma em um grupo, e nossos grupos adimensionais ficaram assim:

π 1 = d   a ⋅ ρ   b ⋅ a   c ⋅ μ π 2 = d   d ⋅ ρ   e ⋅ a   f ⋅ K π 3 = d   g ⋅ ρ   h ⋅ a   i ⋅ D

Agora vamos escrever cada um deles em relação às dimensões. Lembrando que nossos coeficientes precisam ser iguais a zero, temos:

L   a ⋅ M L 3   b ⋅ 1 t c ⋅ M L t = 0

Isso nos diz que:

L :       a - 3 b + 0 - 1 = 0

M :         0 + b + 0 + 1 = 0

t :         0 + 0 - c - 1 = 0

Então temos:

b = c =   - 1

Sendo assim teremos:

  a - 3 ⋅ - 1 + 0 - 1 = 0

a = - 2

Portanto nosso primeiro grupo adimensional será:

π 1 = d     - 2 ⋅ ρ   - 1 ⋅ a     - 1 ⋅ μ

π 1 = μ d 2   ⋅   ρ   ⋅   a

Passo 3

Agora vamos fazer o mesmo para o segundo grupo adimensional!

π 2 = d   d ⋅ ρ   e ⋅ a   f ⋅ K

L   d ⋅ M L 3   e ⋅ 1 t f ⋅ L t = 0

Isso nos diz que:

L :       d - 3 e + 0 + 1 = 0

M :         0 + e + 0 + 0 = 0

t :         0 + 0 - f - 1 = 0

Então temos:

e = 0 e f =   - 1

Sendo assim:

d - 3 ⋅ 0 + 0 + 1 = 0

d = - 1

Portanto nosso segundo grupo adimensional será:

π 2 = d   - 1 ⋅ ρ   0 ⋅ a   - 1 ⋅ K

π 2 = K d   ⋅   a

Passo 4

E para fechar, vamos fazer o mesmo para o terceiro grupo adimensional!

π 3 = d   g ⋅ ρ   h ⋅ a   i ⋅ D

L   g ⋅ M L 3   h ⋅ 1 t i ⋅ L 2 t = 0

Isso nos diz que:

L :       g - 3 h + 0 + 2 = 0

M :         0 + h + 0 + 0 = 0

t :         0 + 0 - i - 1 = 0

Então temos:

h = 0 e i =   - 1

Sendo assim:

  g - 3 ⋅ 0 + 0 + 2 = 0

g = - 2

Portanto nosso terceiro grupo adimensional será:

π 3 = d   - 2 ⋅ ρ   0 ⋅ a   - 1 ⋅ D

π 3 = D d 2   ⋅   a

Uhul! Finalizamos!

Resposta

Os grupos adimensionais são:

π 1 = μ d 2   ⋅   ρ   ⋅   a π 2 = K d   ⋅   a π 3 = D d 2   ⋅   a

Exercícios de Livros Relacionados

Interprete o enunciado: para transferir grande quantidade de massa; procura-se reduzir a espessura da camada limite mássica o tanto quanto possível.
Obtenha uma relação de ordem de magnitude para S c ≠ 1 para a distribuição de concentração do soluto via camada limite mássica no regime laminar.
Porque a espessura da camada limite mássica aumenta com a injeção de matéria? Qual é o efeito no fluxo global de massa?
Interprete fisicamente a figura ( 8.6 ) .
Utilizando o diagrama mnemônico, mostre que S t_M = (S_h)/(R_e S C)