Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Análise Dimensional

Ver Teoria
Exercício 61234578

Enunciado

Na transferência de massa por convecção forçada as variáveis pertinentes são: massa específica ρ , comprimento característica l , difusividade de massa D A B = L 2 T - 1 , viscosidade dinâmica ( µ ) , velocidade ( v ) e coeficiente de transferência de massa k c = L T - 1 . Determine os grupos adimensionais sendo que l , ρ e D A B formam o grupo de grandezas repetidas.

Passo 1

Vamos resolver esse probleminha de análise dimensional!

Pra começar vamos separar as variáveis e suas dimensões, ok?

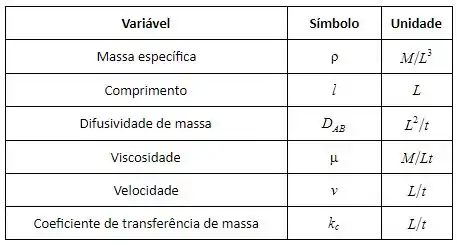
Temos então, seis variáveis e três dimensões primárias , logo:

i = 6 - 3

i = 3

Opa! Então nós vamos ter três grupos adimensionais!

Passo 2

O enunciado já disse pra gente que as grandezas repetidas, serão l , ρ e D A B … Então nossos três grupos ficaram assim:

π 1 = l   a ⋅ ρ   b ⋅ D A B   c   ⋅ μ π 2 = l   d ⋅ ρ   e ⋅ D A B   f   ⋅ v π 3 = l   g ⋅ ρ   h ⋅ D A B   i   ⋅ k c

Agora vamos escrever cada um deles em relação às dimensões. Lembrando que nossos coeficientes precisam ser iguais a zero, temos:

L   a ⋅ M L 3   b ⋅ L 2 t c ⋅ M L t = 0

Isso nos diz que:

L :       a - 3 b + 2 c - 1 = 0

M :         0 + b + 0 + 1 = 0

t :         0 + 0 - c - 1 = 0

Então temos:

b = c =   - 1

Sendo assim teremos:

a - 3 ⋅ - 1 + 2 ⋅ - 1 - 1 = 0

a = 0

Portanto nosso primeiro grupo adimensional será:

π 1 = l   0 ⋅ ρ   - 1 ⋅ D A B   - 1   ⋅ μ

π 1 = μ ρ ⋅ D A B

Passo 3

Agora vamos fazer o mesmo para o segundo grupo adimensional!

π 2 = l   d ⋅ ρ   e ⋅ D A B   f   ⋅ v

L   d ⋅ M L 3   e ⋅ L 2 t f ⋅ L t = 0

Isso nos diz que:

L :       d - 3 e + 2 f + 1 = 0

M :         0 + e + 0 + 0 = 0

t :         0 + 0 - f - 1 = 0

Então temos:

e = 0 e f =   - 1

Sendo assim:

d - 3 ⋅ 0 + 2 ⋅ - 1 + 1 = 0

d = 1

Portanto nosso segundo grupo adimensional será:

π 2 = l   1 ⋅ ρ   0 ⋅ D A B   - 1   ⋅ v

π 2 = v ⋅ l D A B

Passo 4

E para fechar, vamos fazer o mesmo para o terceiro grupo adimensional!

π 3 = l   g ⋅ ρ   h ⋅ D A B   i   ⋅ k c

L   g ⋅ M L 3   h ⋅ L 2 t i ⋅ L t = 0

Isso nos diz que:

L :       g - 3 h + 2 i + 1 = 0

M :         0 + h + 0 + 0 = 0

t :         0 + 0 - i - 1 = 0

Então temos:

h = 0 e i =   - 1

Sendo assim:

  g - 3 ⋅ 0 + 2 ⋅ - 1 + 1 = 0

g = 1

Portanto nosso terceiro grupo adimensional será:

π 3 = l   1 ⋅ ρ   0 ⋅ D A B   - 1   ⋅ k c

π 3 = k c ⋅ l D A B

Uhul! Finalizamos!

Resposta

Os grupos adimensionais são:

π 1 = μ ρ ⋅ D A B π 2 = v ⋅ l D A B π 3 = k c ⋅ l D A B

Exercícios de Livros Relacionados

Interprete o enunciado: para transferir grande quantidade de massa; procura-se reduzir a espessura da camada limite mássica o tanto quanto possível.
Obtenha uma relação de ordem de magnitude para S c ≠ 1 para a distribuição de concentração do soluto via camada limite mássica no regime laminar.
Porque a espessura da camada limite mássica aumenta com a injeção de matéria? Qual é o efeito no fluxo global de massa?
Interprete fisicamente a figura ( 8.6 ) .
Utilizando o diagrama mnemônico, mostre que S t_M = (S_h)/(R_e S C)