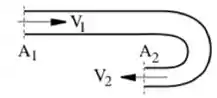
No cotovelo de 180˚ da figura circula agua que é descarregada na seção 2 para a atmosfera. A pressão do medidor é . As áreas são e , a velocidade é . Calcule a força para segurar o cotovelo.
Passo 1
Bom, pra essa questão vai ser melhor se a gente ver o equacionamento antes de começar a resolver. Com ele a gente vai vendo o que podemos simplificar e como vamos resolver cada coisa!
Como o problema está pedindo pra gente a força no eixo x, já é um indicativo de que vamos usar a equação da conservação da quantidade de movimento!
Passo 2
Vamos então ver o que que a gente pode cortar dai!
A gente vai considerar estado estacionário, porque o fluxo de água no cotovelo é contínuo, então não tem variação ao longo do tempo. Então, esse primeiro termo vai embora = 0 !
Fluido incompressível, então .
pois não tem nenhum fluido externo fazendo arraste de espécie.
E também vamos considerar , como se a gravidade não tivesse afetando nosso problema tanto assim, então o último termo vai embora também. (A gente pode fazer isso porque não tivemos nenhuma informação sobre esse termo).
Nosso balanço ficou então:
Sendo que como temos duas áreas relevantes, a integral sobre a área vai ser a soma da integral pra e .
Passo 3
Vamos resolver cada termo então:
Pela conservação de massas conseguimos achar :
Assim:
Os sinais invertem porque o cotovelo faz 180˚ a gente orienta o vetor normal pra fora da superfície! Ou seja, pra a água está entrando e pra a água está saindo.
Passo 4
O outro termo é um pouco mais complicado porque tem o termo que a gente quer, então vamos ver como é que a gente olha pra ele:
A tensão nesse caso é a mesma coisa que pressão, e elas tem a mesma unidade. Múltiplicada pela área temos unidade de força!
Passo 5
Passo 6
Juntando tudo temos que:
Finalmente:
Lembrando que o sinal é só questão de orientação das superfícies, se tivesse dado negativa nossa resposta a gente poderia responder em módulo