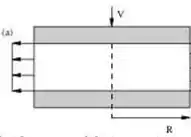
Dois discos planos de raio R são separados por uma distância . O disco superior se move para baixo com velocidade constante . O fluido entre os dicos é comprimido e escorre na direção radial. Determine a taxa volumétrica e a velocidade do fluido considerando o perfil de escoamento uniforme.
Passo 1
Bom, vamos então ver aquele passo a passo!
- Definir a geometria do problema: Volume de Controle e Superfície de Controle
- Montar o equacionamento do problema
- Fazer simplificações baseadas nas considerações que o problema te der
- Analisar a expressão termo a termo, usando essas simplificações
- Juntar tudo e resolver!
Passo 2
Vamos então definir a geometria do nosso problema!
O volume de controle vai ser então o espaço entre os dois discos de raio R, que vai ser um cilindro de altura .
A superfície de controle vai ser uma só, é a superfície envolta do volume de controle, aonde o fluido está escoando.
A gente não leva em consideração as superfícies de cima e de baixo do cilindro (que é como se fosse a parede do disco) porque ali não tem espécie atravessando, beleza?
Passo 3
Vamos montar o balanço de massa então:
Como no nosso caso não está acontecendo transporte de espécie por difusão e nem está acontecendo reação química, a nossa equação se reduz à equação de conservação de massa:
Outra simplificação que podemos considerar também é a densidade constante. Bora então resolver cada um desses termos!
Passo 4
Resolvendo o primeiro termo:
Pra resolver o segundo termo, consideramos , já que não tem nenhum fluido externo fazendo arraste de matéria, quem está escoando é o próprio fluido que estava entre os discos mesmo. E vamo chamar a velocidade do fluido de pra não confundir com a velocidade do disco que está descendo. Sendo assim:
Passo 5
Passo 6
Juntando tudo temos que:
Logo:
Com isso podemos calcular a tava volumétrica!
Passo 7
Calculando a taxa: