Na tubulação da figura corre um fluido imcompressível. Considerando a gravidade, determine a força que o fluido exerce na tubulação.
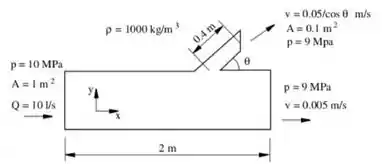
Passo 1
Bom, pra essa questão vai ser melhor se a gente ver o equacionamento antes de começar a resolver. Com ele a gente vai vendo o que podemos simplificar e como vamos resolver cada coisa!
Como o problema está pedindo pra gente a força que o fluido faz no tubo, já é um indicativo de que vamos usar a equação da conservação da quantidade de movimento!
Passo 2
Vamos então ver o que que a gente pode cortar dai!
A gente vai considerar estado estacionário, porque o fluxo de líquido é contínuo, então não tem variação ao longo do tempo. Então, esse primeiro termo vai embora = 0 !
Fluido incompressível, então .
pois não tem nenhum fluido externo fazendo arraste de espécie.
E vamos considerar , pois o problema pede para considerar a ação da gravidade.
Nosso balanço ficou então:
Passo 3
Vamos agora definir nossa geometria!
Nosso volume de controle vai ser o volume da tubulação princiál mais o volume do canalzinho que tá saindo dali!
As nossas superfícies de controle vão ser as 3 dadas, aonde tem fluido atravessando:
Passo 4
Vamos resolver cada termo então:
Pra encontrar as velocidades:
Como o fluido flui em direções opostas através de e :
Olhando agora pro outro termo:
A tensão nesse caso é a mesma coisa que pressão, e elas tem a mesma unidade. Múltiplicada pela área temos unidade de força!
Passo 5
Passo 6
Juntando tudo temos que:
Finalmente:
Lembrando que o sinal é só questão de orientação das superfícies, se tivesse dado negativa nossa resposta a gente poderia responder em módulo