Dada a viga abaixo e sabendo que essa viga trabalha num local onde sua superfície superior se encontra acima da superfície inferior. Determine o deslocamento vertical do ponto mostrado. Considere a altura da viga e o coeficiente de dilatação linear como:
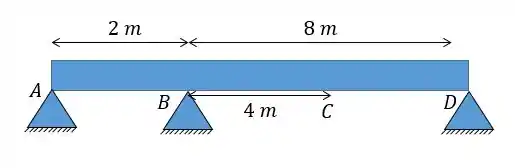
Caso necessário utilize o seguinte diagrama de momento fletor para a carga mostrada:
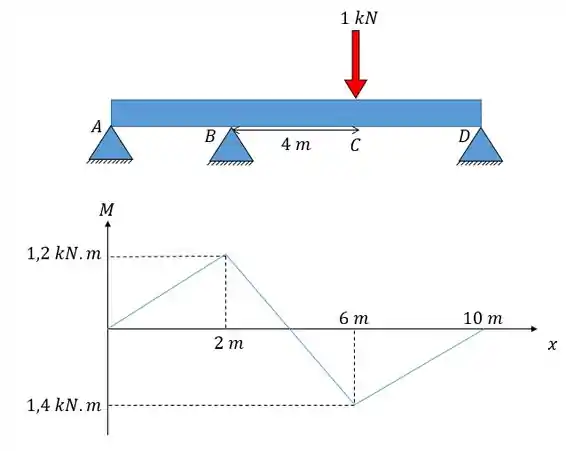
Passo 1
Vamo lá rapaziada marota, partiu resolver mais um exercício de temperatura aplicada à viga. Nesse caso o problema nos fornece uma viga sem carregamento, apenas com a variação de temperatura a qual suas fibras estão sujeitas. Dessa forma ocorrerá uma deflexão exatamente por causa da diferença de dilatação térmica entre as fibras.
Essa deflexão (ou deslocamento) pode ser calculado a partir da seguinte equação:
Então perceba que o problema nos fornece quase todos os dados: nós só temos de encontrar o momento fletor e a normal. Para encontrar esses termos a gente tem que aplicar uma carga unitária no ponto e na direção que queremos descobrir o deslocamento. No caso em questão irá ficar assim:
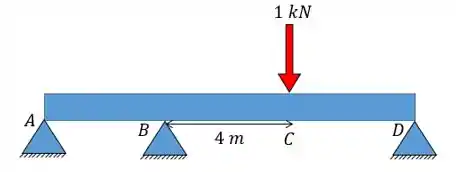
Exatamente o que o problema nos forneceu né? Que bonzinho... hahha
Repara só que o problema deu o diagrama de momento fletor e não forneceu o da normal. Por quê? Porque não tem normal oras... Então a nossa equação vai ficar como:
Lembrando que a gente quer o deslocamento vertical que é dado por , ok?
Acho que já entendemos o problema né? Partiu resolver
Passo 2
Agora vamos dar uma facilitada na nossa expressão:
Nós podemos retirar os termos que são constantes da integral e obter:
Aí todos esses termos que são constantes o problema já forneceu, só falta achar a integral do momento fletor. Mas aqui cabe ressaltar que essa integral vai ser igual à área do diagrama, que o problema também forneceu!!! Ahhh tá muito fácil isso aqui gentemmm..
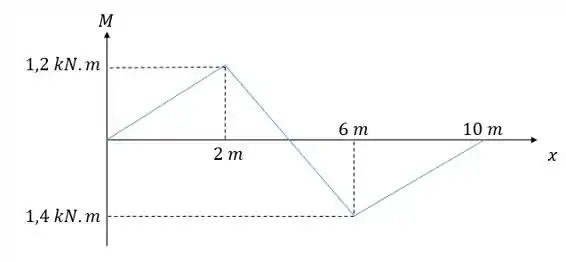
Então vamos achar essa área, para isso vamos ter que achar o ponto de interseção da curva com o eixo , podemos fazer isso por semelhança de triângulos:
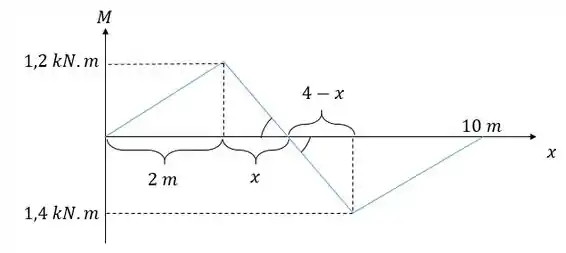
Fazendo a relação entre os lados opostos aos ângulos indicados igual à relação entre as bases vamos ter:
Passo 3
Agora podemos calcular as áreas, assim nós vamos ter:
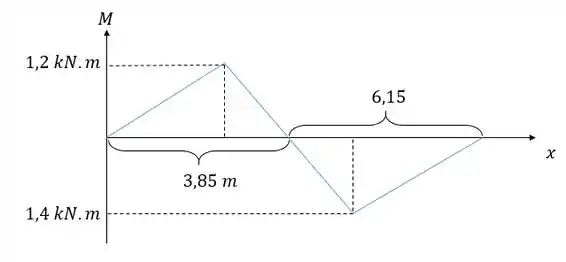
Lembrando que nesse tipo de diagrama o momento fletor negativo é representado acima do eixo , logo as áreas acima desse eixo vão ter um sinal negativo associado.
Passo 4
Agora é só substituir na equação:
Por que para baixo? Porque achamos um valor positivo, ou seja, condizente com a força unitária para baixo.