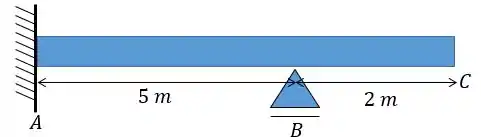
A viga abaixo encontra-se num lugar onde suas fibras inferiores estão a uma temperatura de e as fibras superiores a uma temperatura de . Sabendo que uma força de é aplicada na sua extremidade , calcule o deslocamento dessa extremidade considerando que a distribuição de temperatura é uniforme e que a altura e o coeficiente de dilatação linear são:
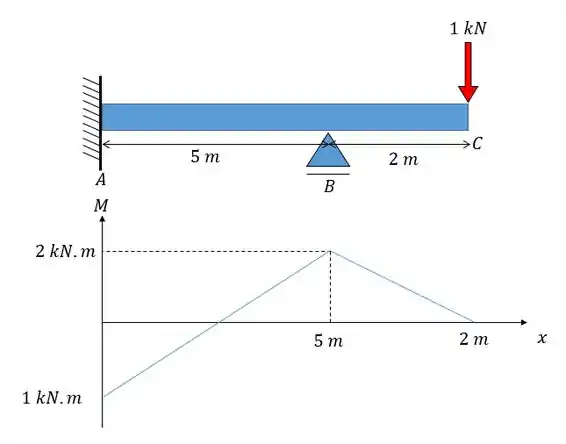
Caso necessite utilize o seguinte diagrama:
Passo 1
Galerinha, essa questão aqui fala mais um pouquinho sobre como a variação de temperatura vai influenciar na deflexão da nossa viga. O problema quer exatamente isso, a deflexão no ponto que é dada pela equação:
Como não há forças normais e também existem vários termos constantes, que podem sair da integral, vamos ter isso aqui:
Todos os termos que são constantes e foram retirados da integral o problema já nos forneceu, e a gente quer achar a deflexão, logo, . Aí é só lembrar que é a nossa força unitária apontada na direção do deslocamento que queremos encontrar (vertical) e é o diagrama de momento fletor referente à essa força , que nos foi dado!!
Então partiu resolver esse probleminha
Passo 2
Como a gente acabou de ver temos quase todos os termos, só não temos a integral. Mas essa integral é igual a área do diagrama:
Então vamos calcular a área desse diagrama:
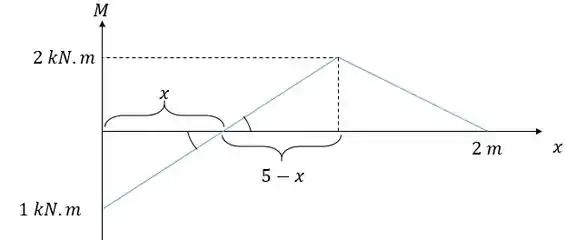
Fazendo semelhança de triângulos nós vamos ter:
Aí a gente só tem que lembrar que as áreas acima do eixo são negativas porque representam momentos fletores negativos, sendo assim:
Passo 3
Agora é só substituir na equação!!
Lembre-se que está apontado para baixo porque condiz com o sentido da força unitária.