Exercícios de Cálculo das deformações devido a temperatura e recalque - Lista de Exercícios Resolvida
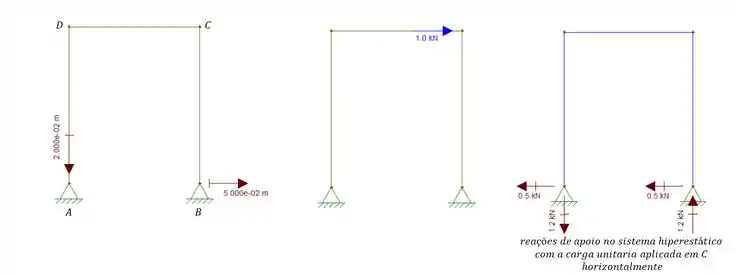
Questão 1
Abaixo nos é dado um pórtico que sofre os recalques mostrados na figura. Sabendo que as reações de apoio dadas são referentes a uma carga untaria aplicada em C na direção horizontal e no sentido mostrado, determine o deslocamento horizontal do ponto C.
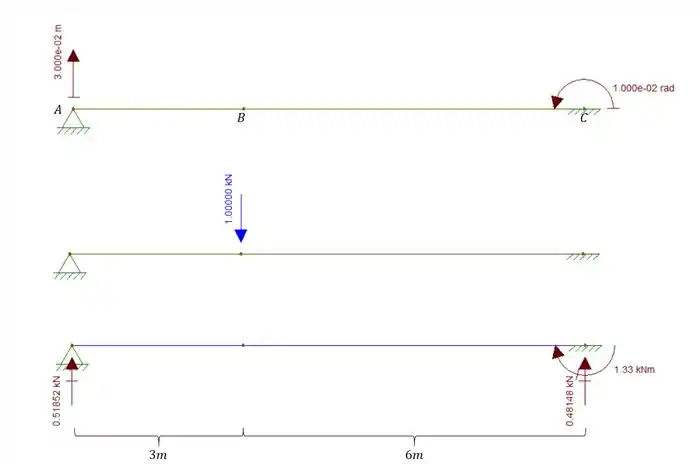
Questão 2
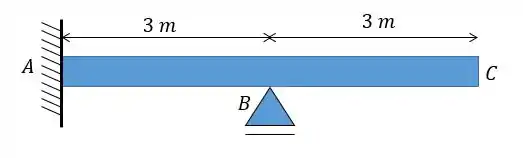
Determine para o ponto B da viga o seu deslocamento vertical. Saiba que na estrutura hiperestática foi usado uma carga unitária vertical em B, que apresentou as reações de apoio mostradas na figura. Assim como os deslocamentos também são mostrados na figura.
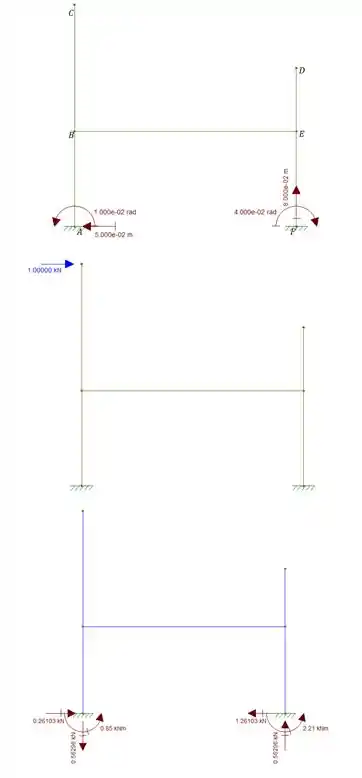
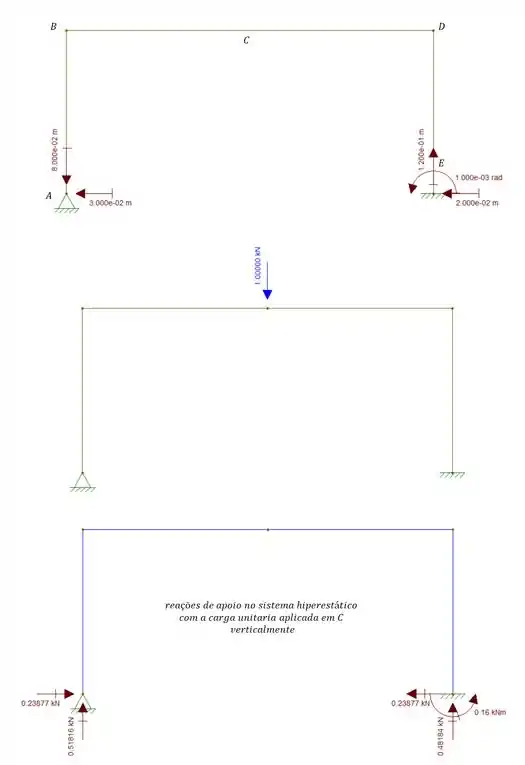
Questão 3
O pórtico abaixo sobre um recalque em A na vertical e para baixo de 8cm e para esquerda de 3cm, e em E, sofre um deslocamento horizontal de 2cm para esquerda, 0.001Rad no sentido anti-horário e 12cm na vertical para cima. Sabendo disso, determine o deslocamento vertical do ponto C.
Questão 4
Dada a viga abaixo e sabendo que essa viga trabalha num local onde sua superfície superior se encontra acima da superfície inferior. Determine o deslocamento vertical do ponto mostrado. Considere a altura da viga e o coeficiente de dilatação linear como:
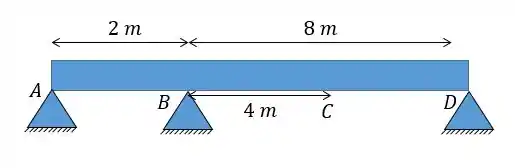
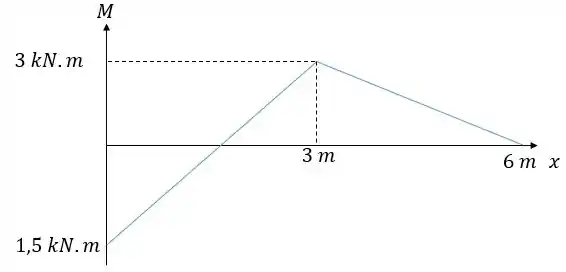
Caso necessário utilize o seguinte diagrama de momento fletor para a carga mostrada:
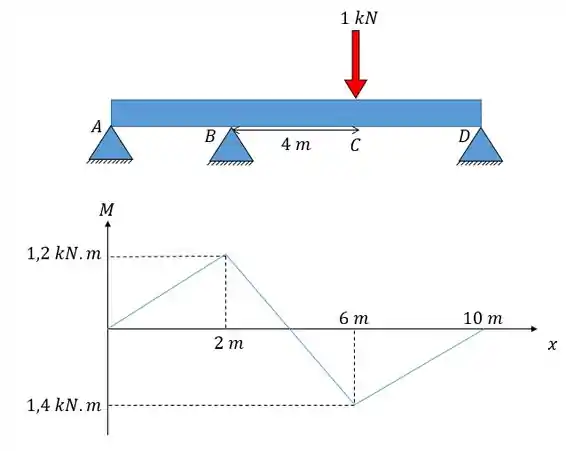
Questão 5
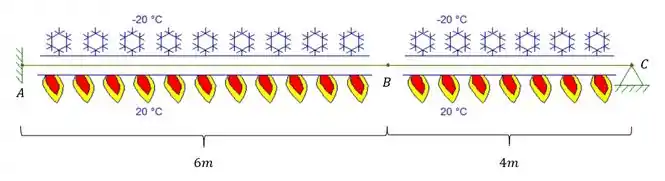
A viga abaixo encontra-se num lugar onde suas fibras inferiores estão a uma temperatura de e as fibras superiores a uma temperatura de . Sabendo que uma força de é aplicada na sua extremidade , calcule o deslocamento dessa extremidade considerando que a distribuição de temperatura é uniforme e que a altura e o coeficiente de dilatação linear são:
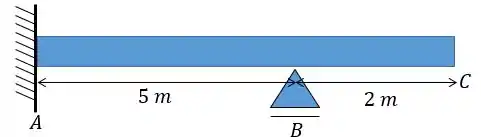
Caso necessite utilize o seguinte diagrama:
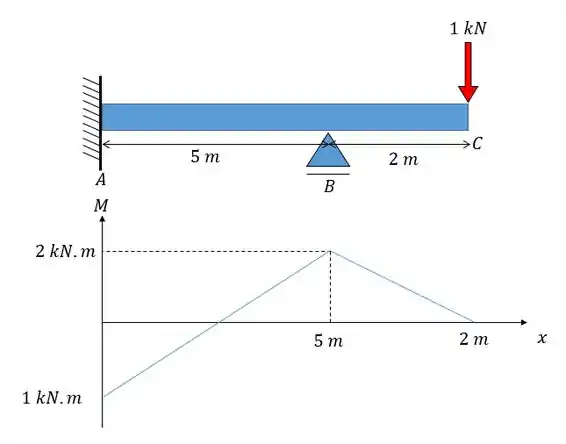
Questão 6
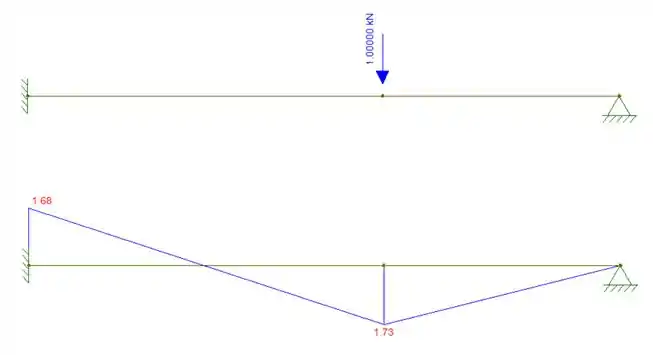
A viga abaixo está sujeita a uma variação de temperatura de 35°C entre suas fibras superiores e inferiores. Sabendo disso e utilizando o diagrama de momento fletor para uma carga unitária vertical apontado para baixo aplicada em , determine o deslocamento vertical do ponto da viga. Supor a altura da viga e coeficiente de dilatação linear como: