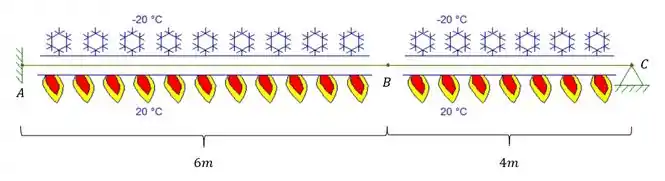
Uma viga possui suas fibras superiores resfriando a -20°C e as inferiores são mantidas a 20°c. sabendo disso e usando os diagramas correspondentes abaixo, determine o deslocamento vertical do ponto B da vida dada abaixo. Supor a altura da viga como
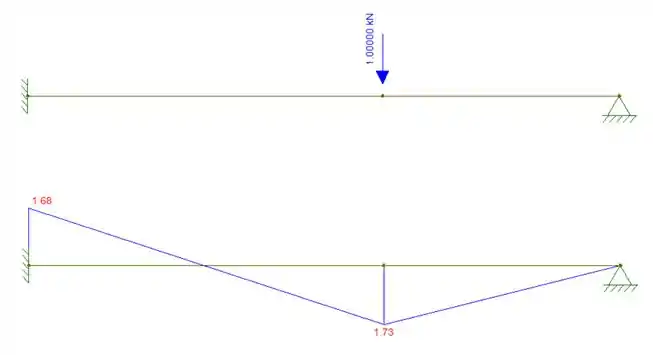
Passo 1
Perceba que aplicamos o carregamento unitário no nosso sistema hiperestático, e obtemos o diagrama de momentos fletores no sistema hiperestático devido a carga unitária.
Em contra partida, sabemos que aplicamos nosso carregamento de temperatura no sistema isostático, e que a fórmula que devemos usar é dada por:
E perceba, se tirarmos das integrais os valores constantes, teremos que:
Em que:
Porém no nosso caso de viga, pouco importa o normal, sendo assim, podemos nos concentrar basicamente nos momentos fletores, e como podemos ver, na área do diagrama de momentos fletores, e perceba, será exatamente a área do diagrama de momentos fletores devido a carga unitária no sistema hiperestático.
Sendo assim nossa fórmula será:
E podemos fazer uma regra de 3 no nosso diagrama:
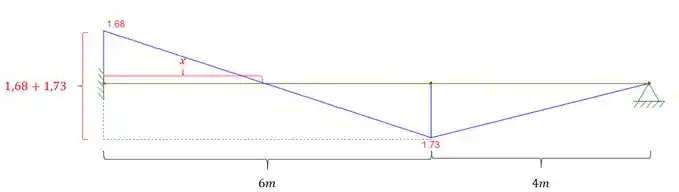
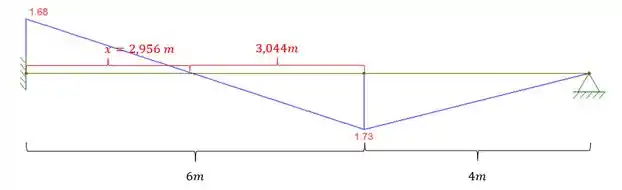
Sabemos que para determinar a área precisamos respeitar o sinal do momento, ou seja, tudo acima do eixo da viga é considerado negativo, e tudo que está abaixo é considerado positivo, e assim teremos que:
Olhando a nossa equação teremos que:
Substituindo teremos que: