O pórtico abaixo sobre um recalque em A na vertical e para baixo de 8cm e para esquerda de 3cm, e em E, sofre um deslocamento horizontal de 2cm para esquerda, 0.001Rad no sentido anti-horário e 12cm na vertical para cima. Sabendo disso, determine o deslocamento vertical do ponto C.
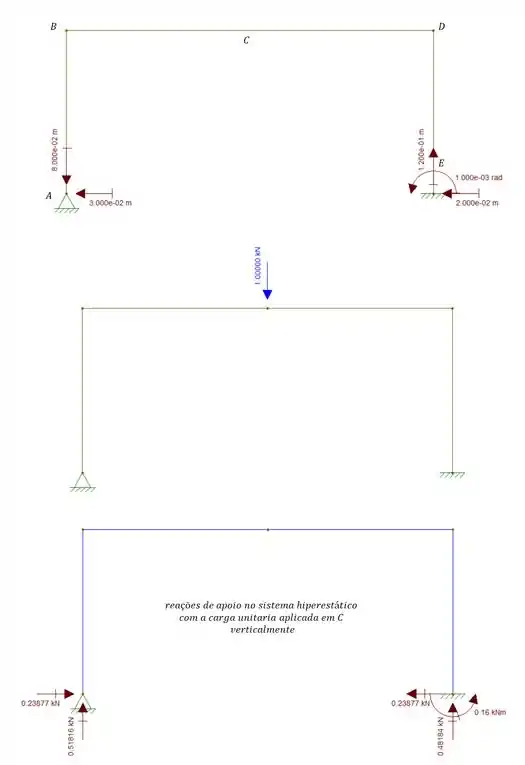
Passo 1
Se olharmos o nosso desenho vamos perceber que o diagrama de reações de apoio com a carga unitária que nos foi dado é na estrutura hiperestática. Ou seja, é como se os carregamentos de recalque fossem aplicados na estrutura isostática, que já sabemos antecipadamente que produzira um diagrama zero. E como aplicamos a carga unitária na estrutura hiperestática, no ponto e na direção que queríamos saber o recalque, vamos ter que:
Em que:
Olhando a nossa estrutura vamos ter que:

- No apoio em A temos um deslocamento de 8cm para baixo e uma reação de para cima, e como estão em direções opostas, o sinal será negativo.
- Ainda no apoio A temos um deslocamento de 3cm para esquerda e uma reação de apoio de para direita, como estão em sentidos opostos, serão novamente negativos.
- Indo para o apoio E, vemos um deslocamento de rotação de e uma reação de apoio no mesmo sentido anti-horário dado por , mas como fazemos as contas em cm, vamos mudar a unidade que vai ser . Logo essa combinação será positiva
- No apoio E também temos um deslocamento vertical de , e uma reação de apoio no mesmo sentido de . Logo essa combinação será positiva.
- E por fim no apoio E ainda temos um deslocamento de para a esquerda, com uma reação de apoio na mesma direção de . Logo essa combinação será positiva também.
Perceba que o deslocamento deu negativo, ou seja, é o oposto ao que supomos para a carga unitária, ou seja, o ponto C desloca, , para cima.