Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de densidades volúmétricas, planares e lineares em células unitárias

Ver Teoria
Exercício 41235678

Enunciado

Calcule o raio de um átomo de ouro, que apresenta uma estrutura cristalina C C C e massa especifica de 19 ,   32 g c m 3 e um peso atômico de 196,96 g m o l .

Passo 1

Primeiramente vamos definir como calcular o volume da célula unitária. Para o cálculo do volume temos:

V =   a ³

Sendo “a” o parâmetro de rede, onde temos:

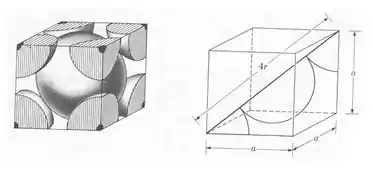
Por Pitágoras, do triângulo retângulo no interior do cubo, tiramos

a 2 2 + a 2 = 4 r 2

2 ∙ a 2 + a 2 = 4 2 ∙ r 2

3 ∙ a 2 = 4 2 ∙ r 2

a 2 = 4 2 ∙ r 2 3

a 2 3 2 = 4 2 ∙ r 2 3 3 2

a 2 ∙ 3 2 = 4 2 ∙ 3 2 ∙ r 2 ∙ 3 2 3 3 2

a 3 = 4 3 ∙ r 3 3 3

V = 64 ∙ r 3 3 3

Passo 2

Para determinarmos o raio temos de utilizar a fórmula da densidade teórica:

ρ = n A V C N a

Onde:

  • n = número de átomos= 2
  • A = massa atômica = 196 ,   96 g m o l
  • V C = volume da célula unitária = 64 ∙ r 3 3 3
  • N a = número de Avogadro 6,02   ∙   10 23

Achando R:

ρ = n ∙ A 64 ∙ r 3 3 3 ∙ N a

ρ = n ∙ A ∙ 3 3 64 ∙ r 3 ∙ N a

64 ∙ r 3 ∙ N a ∙ ρ = n ∙ A ∙ 3 3

r 3 = n ∙ A ∙ 3 3 64 ∙ N a ∙ ρ

r = n ∙ A ∙ 3 3 64 ∙ N a ∙ ρ 1 3

Substituindo:

r = 2 ∙ 196,96 ∙ 3 3 64 ∙ 6,02   ∙   10 23 ∙ 19,32 1 3

r = 1,40 ∙ 10 - 8   c m

Resposta

r = 1,40 ∙ 10 - 8   c m

Exercícios de Livros Relacionados

Para um monocristal CCC, você esperaria que a energia de superfície para um plano (100) fosse maior ou menor que para um plano (110)? Por quê? (Nota: Se necessário, consulte a solução para o Problema
A concentração de carbono em uma liga ferro-carbono é de 0,15%p. Qual é a concentração em quilogramas de carbono por metro cúbico da liga?
Determine o número do tamanho do grão ASTM se são medidos 20 grãos por polegada quadrada sob uma ampliação de 50 × .
O germânio forma uma solução sólida substitucional com silício. Calcule o número de átomos de germânio por centímetro cúbico para uma liga de germânio-silício que contém 15%p Ge e 85%p Si. As massas e
Para uma solução sólida formada por dois elementos (designados por 1 e 2), algumas vezes é desejável determinar o número de átomos por centímetro cúbico de um elemento em uma solução sólida, N 1 , dad