Representação de Números
Teoria
Introdução
Fala moçada, beleza? Vamos dar início ao estudo de uma disciplina muuuuito bacana que é o Cálculo Numérico, o nosso objetivo aqui é estudar o uso de alguns métodos numéricos para resolução dos mais diversos problemas!!! Então fique tranquilo que seus problemas acabaram!
Nós devemos ter em mente que o computador, a máquina, vai fazer tudo para a gente! Ou seja, os métodos que veremos muitas vezes vão parecer cansativos e demorados se nos imaginarmos resolvendo eles, mas normalmente são moleza para uma máquina.
E por mais que uma máquina faça todas as contas para nós, nós nunca conseguimos nos livrar de um detalhe bem incômodo: os erros. Vamos falar muito deles nesse curso pois seu entendimento é super necessário para conseguirmos aplicar os métodos numéricos adequadamente.
Algarismos significativos
Antes de começar a estudar como os números são apresentados para as máquinas, vamos relembrar um assuntinho que nos acompanha desde o início dessa jornada nas Engenharias e Ciências Exatas. Consegue dar um palpite? Se você chutou Algarismos significativos, você está certíssimo.
Veja bem, os algarismos significativos de um número são aqueles que podem ser usados com confiança e geralmente corresponde ao número de algarismos corretos mais um estimado, também chamado de duvidoso, e esse algarismo duvidoso carrega com ele uma incerteza e é nela que mora o erro.
Observe a marcação em nossa régua, quantos centímetros ela está medindo?
Bom, podemos afirmar com certeza que ela está medindo mais que 2,2 e menos que 2,3 cm. O número exato que procuramos existe e mora no intervalo entre esses números, mas não podemos identificá-lo com certeza absoluta, não é?
Podemos colocar esse número mais perto do ou mais perto do . Mas qual vai estar certo? Não podemos afirmar nada...
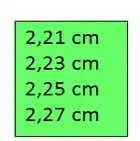
Então, temos uma incerteza aí! E isso está dependendo do observador ou do equipamento que você está usando para tirar essa medida.
No exemplo acima, cada estimativa tem 3 algarismos significativos, eles podem ser algarismos corretos ou duvidosos. Temos certeza, que o número que procuramos está entre e ou seja o número é tem 2 algarismos corretos e estamos em dúvida quanto ao terceiro. Podemos considerar este último mais perto do ou mais perto do .
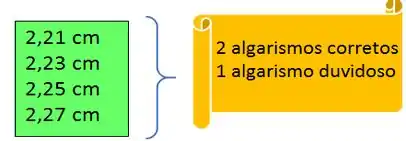
Nesse caso acima, estamos com 3 algarismos significativos e nossa incerteza é da ordem de . Isso porque podemos considerar mais perto do ou mais perto do .
Vamos ver como funciona, quantos algarismos significativos tem o número 31.400? Ele pode ter 3, 4 ou 5 algarismos significativos, dependendo de os zeros serem conhecidos com confiança.
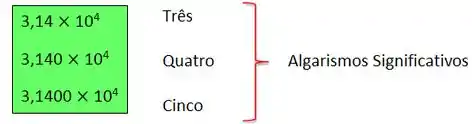
Perceba bem que todas essas representações podem ser apresentadas na forma de notação científica e um computador representa um número real no sistema próprio denominado aritmética de ponto flutuante resolvendo toda a incerteza!
Representação de Números
Tudo que usarmos vai depender de você, da sua necessidade. Vamos ver como isso interfere nos resultados?
Número máximo de dígitos ()
Imagine que você quer calcular a área de um disco de raio igual a .
Você pode dar várias respostas e ainda assim todas estão erradas! Algumas respostas possíveis seriam:
Enfim, você pegou o espírito da coisa né? Como o e um número com infinita casas decimais nunca chegaremos a resposta exata. O resultado que obtemos vai depender exclusivamente da aproximação de que usarmos. E essa aproximação deve ser tão exata quanto precisarmos. E essa ideia será muito importante!
O número de casas decimais a ser usado vai depender da precisão desejada e de onde você vai aplicar esses dados!
Base escolhida
Como nós representamos números? É sobre isso que vamos falar nessa parte.
Cara, a base nada mais é do que a quantidade de algarismos que podemos usar para representar os números. Estamos acostumados com a base decimal que possui 10 algarismos (0, 1, 2... 9), essa é a base com a qual estamos acostumados a lidar no nosso dia a dia e aprendemos desde pequenos. Mas um computador, por outro lado, normalmente usa um sistema de representação binário (0 ou 1), o que significa que o computador irá escrever os números apenas com os algarismos 0 e 1, ele também usa o ponto para representar a nossa vírgula no sistema decimal.
E você pode usar qualquer base que queira para representar os números! A decimal é a mais empregada atualmente, mas existe a binária, a base hexadecimal (base 16), a octal (base 8), entre outras.
E os erros só aumentam quando manipulamos os números em diversas bases. Por exemplo, um número pode ter representação finita em uma base e não-finita em outra (não se preocupe, isso será visto mais pra frente)! Na nossa interação com o computador, nós passamos as informações para ele pelo sistema decimal. Esses dados são convertidos para o binário, no qual todos os cálculos são feitos e depois convertidos de volta para decimal para que possamos ler. Todas essas conversões geram ainda mais erros!
Conversão de Números nos Sistemas Decimal e Binário
Vamos começar engatinhando.
No sistema decimal, para representar um número podemos escrever ele na forma de somas potências de base dez. Parece complicado, mas olha só:
Vamos analisar o número que é do sistema decimal:
Prontinho, escrevemos um número como uma soma de potências de base dez.
Um número escrito na forma binária só usa algarismos do tipo 0 e 1. Mas, da mesma forma que era na base decimal, os algarismos vão indicar uma soma de potências de base dois Por exemplo, vamos agora analisar um número 1011 escrito na base 2:
Entendeu como funciona? Todos os números podem ser escritos como uma soma de potências de uma base. Generalizando, um número com os algarismos na base seria:
Mas por que eu to falando isso? Porque assim é fácil passarmos números do sistema binário pro decimal! Por exemplo o em decimal fica:
Fazendo essas continhas temos:
Então o número da base 2 equivale ao na base dez.
E pra voltar? Ir do decimal para o binário? Aí o que nós vamos fazer é dividir o número por várias vezes até aparecer o no quociente e ir anotando os restos! Assim oh:
Agora escrevemos os restos de trás pra frente:
Percebeu que tá batendo certinho com o que tínhamos? Até aí tudo nas mil maravilhas né?
Mas, e para convertermos os números que vem depois da vírgula? Como faz??
Bom, vamos começar indo do binário para o decimal que é mais fácil, os números depois do ponto (que correspondem a vírgula no sistema decimal) serão elevados a potências de dez negativas. O expoente sempre irá diminuir:
Ou seja, quando temos casas decimais ficamos com:
Então o processo binário decimal não mudou muito né? É só continuarmos diminuindo as potências de .
E para irmos do decimal para o binário? Vamos usar o . Primeiro fazemos a parte inteira:
Beleza, agora para a parte depois da vírgula nós vamos multiplicar por ao invés de dividir! Depois de multiplicar verificamos se o número é maior que . Se for, coloca-se na parte fracionária e o “resto” passa adiante. Caso contrário, botamos um . E vamos fazendo isso até chegarmos no . Vai ficar mais claro com o exemplo:
Pronto, ah e aqui a gente lê na ordem certa haha.
Somando:
Exatamente o que a gente esperava!
Agora lembra aquela história que eu falei de números que são finitos em uma base e não finitos em outra? Vamos passar o número para binário. O já sabemos que fica , mas e o ?
Opa, percebeu que entramos em um loop? Voltamos para o ! Então nosso número em binário será uma dízima:
E é daí que alguns problemas aparecem. . .
Para compreendermos como irá funcionar nesses casos, precisaremos entender um pouco melhor sobre a linguagem que os computadores usam. Isso veremos no próximo tópico, beleza?! Mas antes vamos praticar um pouco de conversão?!
Representação de Números
Conversão de Números nos Sistemas Decimal e Binário
Exercícios Resolvidos
Exercício Resolvido #1
Adaptado do Exemplo 1.4 de Darezzo, S.A.|. A. Cálculo Numérico: aprendizagem com Apoio de Software.
Transforme os seguintes números da base decimal para a base binária:
(a) 25 (b) 11
Passo 1
- 25
- 11
Fala meu amigo, vamos relembrar um pouquinho como trocamos a base de um algarismo:
Vamos do decimal para o binário? Aí o que nós vamos fazer é dividir o número por várias vezes até aparecer o no quociente e ir anotando os restos! Assim oh:
Organizando direitinho os restos fica:
(1)
(0)
(0)
(1)
(1)
Agora lemos os restos de trás pra frente:
Molezinha! Vamos pro próximo?
Passo 2
Meu bem, o esqueminha pra resolver esse exercício é igualzinho ao anteror. Vamos ver como fica?
Organizando direitinho os restos fica:
(1)
(1)
(0)
(1)
Agora lemos os restos de trás pra frente:
Feshooooow! Agora é só partir pro abraço!
Resposta
Exercício Resolvido #2
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 22, exercício 1.
Converta os seguintes números decimais para sua forma binária:
Passo 1
Tá! Vamos lá!
Passo 2
Passo 3
Como só tem parte decimal começamos por ela direto. Lembrando que agora temos que multiplicar e não dividir!
Já deu pra perceber que isso não vai parar tão cedo né? Isso se parar! Então podemos dar como resposta:
Resposta
Exercício Resolvido #3
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 22, exercício 2.
Converta os seguintes números binários para sua forma decimal:
Passo 1
Passo 2
Passo 3
Passo 4
Resposta
Exercício Resolvido #4
Fonte do Exercício.“Elaboração Própria”
Julgue a afirmação abaixo como verdadeiro ou falso:
“Na estrutura de um programa em Matlab, as instruções contêm expressões, que por sua vez, criam e processam matrizes.”
Passo 1
Opa, para resolver essa questão vai ajudar se a gente se lembrar que o nome do Matlab é um acrônimo para Matrix Laboratory, ou seja, laboratório de matrizes.
Então a base do Matlab são as matrizes!
E sim, é verdade que quando você realiza qualquer operação no Matlab, por traz da sua sintaxe você tá criando e operando matrizes.
Então essa resposta é Verdadeira.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Lista 1 – Professora Luziane – UFRJ – Questão 4 Adaptada
Considere um computador que opera em base , com representação em precisão simples. Em cada um dos itens abaixo, mostre qual é o número real que está representado em forma de ponto flutuante normalizado.
Passo 1
O segundo bloco de números representa o expoente. Nele, temos n= 8 espaços, que são 8 bits. Dessa forma, o expoente máximo é dado por:
Assim, a representação normalizada será:
Então o número sendo representado é:
Passo 2
Repare que aqui temos toda a característica cheia de , mas a mantissa diferente de zero. Isso é um caso onde a máquina acusaria (not a number).
Passo 3
Aqui temos expoente todo no e a mantissa zerada. Como , essa seria a representação de .
Passo 4
Como temos expoente igual a e uma mantissa diferente de , isso indica um número não normalizado. Consideramos então a mantissa entre e e expoente mínimo ficando com:
Então o número sendo representado é:
Passo 5
Temos o expoente e a mantissa zerada. Como , essa seria a representação de .
Passo 6
Então o número sendo representado é:
Passo 7
Resposta
Exercício Resolvido #6
Elaboração Própria
Considere um computador de com expoente máximo e a representação em aritmética flutuante na base .
Determine o menor número positivo normalizado e não normalizado representável nesta máquina, na base .
Determine o maior número positivo representável nesta máquina, na base .
Passo 1
Antes de qualquer coisa temos que descobrir quantos essa máquina reserva para cada coisa. Temos pro sinal. Para que o expoente máximo seja , usando nossa relação:
Logo, temos para o expoente.
Ficamos então com:
Logo, para a mantissa.
Passo 2
O menor número normalizado representável seria:
Equivalente em decimal a:
Já o menor número não normalizado seria:
Equivalente a:
Passo 3
O maior número positivo representável é:
O que equivale a:
Resposta
Menor número positivo normalizado:
Menor número positivo não normalizado:
Maior número positivo:
Exercício Resolvido #7
Lista 1 – Professor Raymundo – UFRJ – Questão 10a
Seja um computador binário, cujo sistema de ponto flutuante tenha para o sinal do número, para o expoente e para a mantissa num total de . Qual o menor número positivo e o maior número positivo nele representável.
Passo 1
Como temos para o expoente, o expoente máximo é dado por:
Portanto, o expoente mínimo será .
Também podemos pensar que a máquina vai do expoente até o , ou seja, do ao . Como queremos representar os números negativos também, subtraímos , de modo que os expoentes agora variam de até .
Passo 2
Para obter o maior número, devemos ter o maior expoente e a maior mantissa.
- O maior expoente: 15
- A maior mantissa: f= 0. (111111)
Colocando a mantissa na base decimal:
O valor máximo é dado por:
Sendo assim, o valor máximo que ela pode representar é:
Passo 3
O valor mínimo normalizado é dado por:
- O menor expoente: -14
- A menor mantissa: f= . (000000)
Observação: Só podemos ter essa mantissa toda 0 porque o valor normalizado já conta com um dígito 1 antes da vírgula.
Assim, o valor mínimo normalizado será:
Passo 4
O valor mínimo não normalizado é bem parecido, mas tem a seguinte diferença: não tem aquele 1 antes da vírgula. Então, para obter o valor mínimo, devemos considerar 0 antes da vírgula e o máximo de 0s possíveis na mantissa, colocando 1 apenas no dígito de menor valor. Assim:
- A menor mantissa: f= 0. (000001)
Passando a mantissa para a base decimal:
Assim, o menor valor não normalizado é dado por:
Resposta
Maior número positivo:
Menor número positivo normalizado:
Menor número positivo não normalizado:
Exercício Resolvido #8
Adaptado da lista “Cálculo Numérico (ST462B/ST468B) Lista de exercícios 1 - Representação numérica e Erros” da Unicamp
Considere uma máquina cujo sistema de representação de número é definido por: 𝛽 = 10, 𝑘 = 4,𝑒 ∈ [−5,5]. Pede-se:
(a) Qual o menor e o maior número em módulo representados nesta máquina?
(b) Como será representado o número 73,758 nesta máquina, se for usado o arredondamento? E se for usado o truncamento?
Passo 1
(a) Qual o menor e o maior número em módulo representados nesta máquina?
Opaa, chega mais ! Vamos começar com esse exercício que parece moleza mas é cheio de detalhes. Tem um palpite de como se começa??
Veja bem, que informações o exercício nos dá? O problema nos fornece a base, o número máximo de algarismos que vamos colocar na mantissa e os valores mínimos e máximos de expoente (no intervalo de -5 até 5).
Então, vamos relembrar aquela estrutura que pode ser montada só com as informações que nós temos:
Sabendo que:
Nós conhecemos o valor de
Então, considerando a inequação acima podemos determinar o primeiro valor de
Que pode deve estar entre 1 e 9.
Fácil né? Então significa que podemos variar o nosso valor de (0,1....) até (0,9...).
O exercício fornece que k= 4, então nossos valores de d serão: , .
Para montar a estrutura do menor valor que a máquina pode registrar, devemos considerar que o primeiro dígito (qualquer zero a esquerda acaba sendo reconsiderado e reorganizado e vai parar laaaaaaaaaaaá no expoente) , e como determinamos ali encima ele deve estar entre 1 e 9.
Como o menor valor entre 1 e 9, é o próprio 1 nosso assumirá essa forma.
Beleza, o e n= [-5,5].
A escolha do menor expoente é bem intuitiva né, qual é o menor valor -5 ou 5?
O menor valor é -5, heheheh
Agora é só montar aquela estrutura show de bola:
Lembra, nós temo as base, expoentes e . Mano, agora é só completar!!
O menor número, em valor absoluto, representado por essa máquina seria:
Enquanto o maior número seria:
Moleza né???
Vamos para o próximo passo!
Passo 2
(b) Como será representado o número 73,758 nesta máquina, se for usado o arredondamento? E se for usado o truncamento?
Ao organizarmos o número 73,758 no formato da aritmética de ponto flutuante, fica mais ou menos assim:
Mas, nós temos que deixar com a quantidade correta de números dentro da mantissa que foi sugerida pelo exercício de k= 4.
Vamo simbora!
Só dando uma relembrada como eu faço o arredontamento?
O arredondamento com k dígitos é dado por:
Se arredondamos para cima.
Se arredondamos pra baixo!
Legal, foca nesse número , a certeza que temos está em 0,737X , com 3 algarismos significativos e o último duvidoso!
E agora observe bem: o próximo algarismo em e então arredondamos para CIMA!
Então, com a técnica de arredondamento fica assim:
No truncamento fica como?
No truncamento nós terminamos em
Observe que temos:
Ao para em para fazer o truncamento, fica assim:
Resposta
- Mínimo:
- Arredondamento :
Máximo:
Truncamento :
Exercício Resolvido #9
Lista 1 – Professor Daniel – UFRJ – Questão 3
Considere uma máquina com sistema de representação de números definido por: base , dígitos na mantissa e expoente no intervalo . Como será representado o número nesta máquina se for usado o arredondamento. E se for usado o truncamento?
Passo 1
Nosso instinto já manda a gente fazer o que? Passar pra binário né? Mas presta atenção no que o enunciado fala!! Ele diz que a máquina funciona na base ! Então não tem que passar nada pra nada haha. É só passar pra notação normalizada de ponto flutuante:
Usando o truncamento temos:
E usando o arredondamento:
Resposta
Truncamento:
Arredondamento:
Exercício Resolvido #10
Lista 1 – Professor Raymundo – UFRJ – Questões 3 até 7
Um computador armazena números reais utilizando para o sinal do número, para o expoente e para a mantissa. Admitindo que haja arredondamento, como ficariam armazenados os seguintes números decimais?
Em seguida, responda:
Qual o valor verdadeiramente representado em cada caso acima?
Qual o maior e o menor número positivo nele representável?
Qual o menor número maior que nele representável?
Qual o maior número menor que nele representável?
Passo 1
Os do expoente variarão de até , isto é, de até . Como precisamos representar expoentes negativos, subtraímos disso de modo que o expoente agora varie de até .
Passando o número para binário.
Então, . Repare que esse na frente do binário é aquele que sempre somamos e está implícito. Na hora de passar ele para a representação passamos só o que ficou depois da vírgula. Além disso, como temos mantissa e casas decimais, não precisaremos cortar nenhuma.
Quanto ao expoente , precisamos somar aqueles que calculamos para obtermos o expoente certo.
A representação no sistema será:
Passo 2
Passando o número para binário. Primeiro a parte inteira:
Agora a parte fracionária:
Então, . Temos mantissa e casas decimais, então não precisaremos cortar nenhuma.
Consertando o expoente:
A representação no sistema será:
Passo 3
Passando o número para binário. Primeiro a parte inteira:
Agora a parte fracionária:
Então, . Temos mantissa e casas decimais, então basta cortar as duas últimas. Como o que vai ser cortado é menos da metade da última casa decimal é só tirar mesmo. É importante lembrarmos também que agora o primeiro dígito será um , já que o número é negativo.
Consertando o expoente:
A representação no sistema será:
Passo 4
Passando o número para binário.
Opa, estamos repetindo, então temos uma dízima!
Logo, . Temos na mantissa e infinitos no nosso número, então temos que cortar. Mas agora o que vamos remover é maior que a metade da última casa decimal que vai ficar, então somamos nela, que foi o que eu fiz ali em cima. E novamente temos um número negativo, então primeiro dígito .
Consertando o expoente:
A representação no sistema será:
Passo 5
Passando o número para binário. Primeiro a parte inteira:
Agora a parte fracionária:
Opa, estamos repetindo, então temos uma dízima!
Logo, . Novamente temos na mantissa e infinitos no nosso número, então temos que cortar. E caímos na mesma situação da última letra, na qual o que vamos remover é maior que a metade da última casa decimal que vai ficar, então somamos nela. Por fim, como o número é negativo, então o primeiro dígito é .
Consertando o expoente:
A representação no sistema será:
Passo 6
Passando o número para binário. Primeiro a parte inteira:
Agora a parte fracionária:
Opa, caímos naquele loop do que já sabemos que vai dar uma dízima! É só pegarmos o valor do da outra letra e botarmos um na frente que teremos o resultado do !
Logo, . Temos na mantissa e infinitos no nosso número, então arredondamos.
Consertando o expoente:
A representação no sistema será:
Passo 7
Qual o valor verdadeiramente representado em cada caso acima?
Nas letras em que não arredondamos, o resultado está correto. Nas demais, temos que fazer a conversão:
(valor exato)
(valor exato)
Nessa letra tivemos que cortar as casas decimais. Consequentemente o valor representado foi apenas a parte inteira .
O valor representado foi .
O valor representado foi .
O valor representado foi
Passo 8
Qual o maior e o menor número positivo nele representável?
Maior número positivo:
Menor número positivo na forma normalizada:
Menor número positivo na forma não normalizada:
Passo 9
Qual o menor número maior que nele representável?
Primeiro vamos representar nele:
Então temos que já com as casas decimais da mantissa. O número imediatamente seguinte seria:
Você também poderia reparar que o ocupa da mantissa sobrando apenas para a parte decimal. O menor número fracionário que se pode fazer com é , então o número imediatamente após de nesse sistema tem que ser
Passo 10
Qual o maior número menor que nele representável?
Mesmo esquema da última, vamos representar o :
Então . O número imediatamente anterior seria:
Analogamente ao anterior, o número ocupa da mantissa, sobrando mais para a parte fracionária. A menor fração que podemos fazer nesse caso é . Então o número imediatamente anterior a nesse sistema é
Resposta
.
.
.
Maior número positivo:
Menor número positivo na forma normalizada:
Menor número positivo na forma não normalizada: